题目内容
9.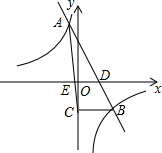 一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A(-1,4),B(2,n)两点,直线AB交x轴于点D.
一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A(-1,4),B(2,n)两点,直线AB交x轴于点D.(1)求一次函数与反比例函数的表达式;
(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.
分析 (1)把A(-1,4)代入反比例函数y=$\frac{m}{x}$可得m的值,即确定反比例函数的解析式;再把B(2,n)代入反比例函数的解析式得到n的值;然后利用待定系数法确定一次函数的解析式;
(2)先由BC⊥y轴,垂足为C以及B点坐标确定C点坐标,再利用待定系数法求出直线AC的解析式,进一步求出点E的坐标,然后计算得出△AED的面积S.
解答  解:(1)把A(-1,4)代入反比例函数y=$\frac{m}{x}$得,m=-1×4=-4,
解:(1)把A(-1,4)代入反比例函数y=$\frac{m}{x}$得,m=-1×4=-4,
所以反比例函数的解析式为y=-$\frac{4}{x}$;
把B(2,n)代入y=-$\frac{4}{x}$得,2n=-4,
解得n=-2,
所以B点坐标为(2,-2),
把A(-1,4)和B(2,-2)代入一次函数y=kx+b得,
$\left\{\begin{array}{l}{-k+b=4}\\{2k+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
所以一次函数的解析式为y=-2x+2;
(2)∵BC⊥y轴,垂足为C,B(2,-2),
∴C点坐标为(0,-2).
设直线AC的解析式为y=px+q,
∵A(-1,4),C(0,-2),
∴$\left\{\begin{array}{l}{-p+q=4}\\{q=-2}\end{array}\right.$,
解$\left\{\begin{array}{l}{p=-6}\\{q=-2}\end{array}\right.$,
∴直线AC的解析式为y=-6x-2,
当y=0时,-6x-2=0,解答x=-$\frac{1}{3}$,
∴E点坐标为(-$\frac{1}{3}$,0),
∵直线AB的解析式为y=-2x+2,
∴直线AB与x轴交点D的坐标为(1,0),
∴DE=1-(-$\frac{1}{3}$)=$\frac{4}{3}$,
∴△AED的面积S=$\frac{1}{2}$×$\frac{4}{3}$×4=$\frac{8}{3}$.
点评 本题考查了反比例函数与一次函数的交点问题,利用待定系数法求反比例函数与一次函数的解析式,三角形的面积,正确求出函数的解析式是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 角是几何图形 | B. | 两平行线间的距离处处相等 | ||
| C. | 对顶角相等吗 | D. | 两个锐角的和是一个直角 |
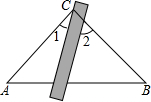 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 35° |
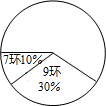 第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:| 命中环数 | 10 | 9 | 8 | 7 |
| 命中次数 | 4 | 3 | 2 | ,1 |
(2)求甲运动员的10次设计的平均成绩是多少环;
(3)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果在这二人中选一人参加比赛,你认为应该派谁去?并说明理由.
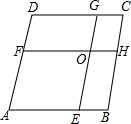 如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )
如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )| A. | 6.5 | B. | 6 | C. | 5.5 | D. | 5 |
 如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )| A. | 236π | B. | 136π | C. | 132π | D. | 120π |
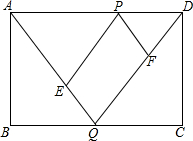 如图,矩形ABCD中,AB=2cm,BC=5cm,两动点P、Q分别同时从顶点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过P作PE∥DQ交AQ于点E,作PF∥AQ交DQ于点F.
如图,矩形ABCD中,AB=2cm,BC=5cm,两动点P、Q分别同时从顶点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过P作PE∥DQ交AQ于点E,作PF∥AQ交DQ于点F.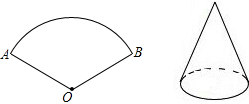 如图,将弧长为6π,圆心角为120°的圆形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是6$\sqrt{2}$.
如图,将弧长为6π,圆心角为120°的圆形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是6$\sqrt{2}$.