题目内容
7. 如图,在平行四边形ABCD中,对角线AC、BD交于O点,AC=6,BD=10,E、F分别是OA、OB的中点.设EF的长为x,则x的取值范围是1<x<4.
如图,在平行四边形ABCD中,对角线AC、BD交于O点,AC=6,BD=10,E、F分别是OA、OB的中点.设EF的长为x,则x的取值范围是1<x<4.
分析 利用平行四边形的性质得出AO,BO的长,进而利用三角形三边关系得出AB的长,进而得出EF的取值范围.
解答 解:∵在平行四边形ABCD中,对角线AC、BD交于O点,AC=6,BD=10,
∴AO=3,BO=5,
∴2<AB<8,
∵E、F分别是OA、OB的中点,EF的长为x,
∴EF=$\frac{1}{2}$AB,
∴1<x<4.
故答案为:1<x<4.
点评 此题主要考查了三角形中位线定理以及三角形三边关系和平行四边形的性质等知识,得出EF=$\frac{1}{2}$AB是解题关键.

练习册系列答案
相关题目
2.有一个三角形的两边是6cm和8cm,要使这个三角形为直角三角形,则第三边的长为( )
| A. | 10cm | B. | $2\sqrt{7}$cm | C. | 10cm或2$\sqrt{7}$cm | D. | 4cm |
12.下列等式变形正确的是( )
| A. | 如果s=vt,那么v=$\frac{t}{s}$ | B. | 如果$\frac{1}{2}$x=6,那么x=3 | ||
| C. | 如果x-3=y-3,那么x=y | D. | 如果a=b,那么$\frac{1}{2}$a=2b |
19.下列语句中不是命题的是( )
| A. | 角是几何图形 | B. | 两平行线间的距离处处相等 | ||
| C. | 对顶角相等吗 | D. | 两个锐角的和是一个直角 |
17.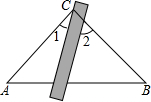 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 35° |
 如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于130°.
如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于130°. 一组合体的三视图如图所示,该组合体是由哪几个几何体组成,并求出该组合体的表面积(单位:cm2).
一组合体的三视图如图所示,该组合体是由哪几个几何体组成,并求出该组合体的表面积(单位:cm2).