题目内容
2.若一组数据x1,x2,x3,x4,x5的平均数为2,方差为$\frac{1}{3}$,则:(1)数据x1-3,x2-3…x5-3的平均数是-1,方差是$\frac{1}{3}$;
(2)数据2x1+1,2x2+1…2x5+1的平均数是5,方差是$\frac{4}{3}$.
分析 (1)根据平均数的变化规律可得出数据x1-2,x2-2,x3-2,x4-2,x5-2的平均数是4-2;先根据数据x1,x2,x3,x4,x5的方差为0.4,即可得出数据x1-2,x2-2,x3-2,x4-2,x5-2的方差;
(2)根据数据的变化和其平均数及方差的变化规律2求得新数据的平均数及方差即可.
解答 解:(1)∵数据x1,x2,x3,x4,x5的平均数是2,
∴数据x1-3,x2-3,x3-3,x4-3,x5-3的平均数是2-3=-1;
∵数据x1,x2,x3,x4,x5的方差为$\frac{1}{3}$,
∴数据x1-3,x2-3,x3-3,x4-3,x5-3的方差是$\frac{1}{3}$;
(2)∵当一组数据中的每一个数据发生什么样的变化其平均数就发生什么样的变化,
∴2x1+1,2x2+1…2x5+1的平均数数据x1,x2,x3,x4,x5的平均数的2倍加1,
∵数据x1,x2,x3,x4,x5的平均数是2,
∴2x1+1,2x2+1…2x5+1的平均数为:2×2+1=5,
∵当一组数据同时加上一个常数不影响方差,
乘以一个常数则其方差变为原来的常数的平方倍,
∴2x1+1,2x2+1…2x5+1的方差为:22×$\frac{1}{3}$=$\frac{4}{3}$.
故答案为:-1,$\frac{1}{3}$;5,$\frac{4}{3}$.
点评 本题考查了方差的定义.当数据都加上一个数(或减去一个数)时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数(或除以一个数)时,平均数也乘以或除以这个数,方差变为这个数的平方倍.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
12.下列等式变形正确的是( )
| A. | 如果s=vt,那么v=$\frac{t}{s}$ | B. | 如果$\frac{1}{2}$x=6,那么x=3 | ||
| C. | 如果x-3=y-3,那么x=y | D. | 如果a=b,那么$\frac{1}{2}$a=2b |
17.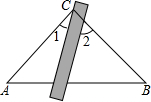 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 35° |
14.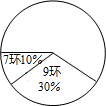 第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
(1)求甲运动员几种7环和10环的次数,并补全扇形统计图;
(2)求甲运动员的10次设计的平均成绩是多少环;
(3)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果在这二人中选一人参加比赛,你认为应该派谁去?并说明理由.
 第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:| 命中环数 | 10 | 9 | 8 | 7 |
| 命中次数 | 4 | 3 | 2 | ,1 |
(2)求甲运动员的10次设计的平均成绩是多少环;
(3)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果在这二人中选一人参加比赛,你认为应该派谁去?并说明理由.
12. 如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
 如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
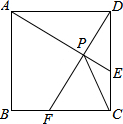 如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动.若AD=2,线段CP的最小值是$\sqrt{5}$-1.
如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动.若AD=2,线段CP的最小值是$\sqrt{5}$-1.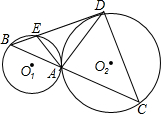 如图,已知⊙O1、⊙O2外切于点A,过点A的直线交⊙O1于B,交⊙O2于C,过点B作直线BD与⊙O1⊙O2分别相交于E,D,连接AE,AD,DC,若AE:AD=ED:DC.
如图,已知⊙O1、⊙O2外切于点A,过点A的直线交⊙O1于B,交⊙O2于C,过点B作直线BD与⊙O1⊙O2分别相交于E,D,连接AE,AD,DC,若AE:AD=ED:DC.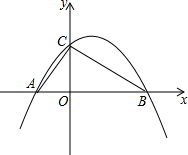 如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.
如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.