题目内容
12.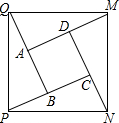 如图,将正方形ABCD的四边各延长一倍.即DM=AD,CN=CD,AQ=AB,BP=BC.连接M,N,P,Q四点,试判断MNPQ的形状,并予以证明.
如图,将正方形ABCD的四边各延长一倍.即DM=AD,CN=CD,AQ=AB,BP=BC.连接M,N,P,Q四点,试判断MNPQ的形状,并予以证明.
分析 由正方形的性质可以得出AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,就可以得出∠MAQ=∠QBP=∠PCN=∠MDN=90°,由条件就可以得出△MAQ≌△QBP≌△PCN≌△NDM,就可以得出MQ=QP=PN=NM,∠PQM=90°,就可以得出结论.
解答 解:四边形MNPQ为正方形.
理由:∵四边形ABCD为正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,
∴∠QAM=∠PBQ=∠NCP=∠MDN=90°.
∵DM=AD,CN=CD,AQ=AB,BP=BC,
∴DM=CN=BP=AQ,
∴AB+AQ=AD+DM=CD+CN=CB+BP,
∴BQ=AM=DN=CP.
在△MAQ和△QBP中
$\left\{\begin{array}{l}{AQ=BP}\\{∠QAM=∠PBQ}\\{BQ=AM}\end{array}\right.$,
∴△MAQ≌△QBP(SAS),
∴MQ=QP,∠AMQ=∠BQP,∠AQM=∠BPQ.
∵∠BPQ+∠BQP=90°,
∴∠AQM+∠BQP=90°,
即∠PQM=90°,
同理可得,△QBP≌△PCN≌△NDM,
∴QP=PN=NM,
∴MQ=QP=PN=NM,
∴四边形MNPQ为菱形.
∵∠PQM=90°,
∴菱形MNPQ为正方形.
点评 本题考查了正方形的性质及正方形的判定的运用,全等三角形的判定及性质的运用,直角三角形的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
2.有一个三角形的两边是6cm和8cm,要使这个三角形为直角三角形,则第三边的长为( )
| A. | 10cm | B. | $2\sqrt{7}$cm | C. | 10cm或2$\sqrt{7}$cm | D. | 4cm |
17.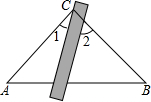 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 35° |
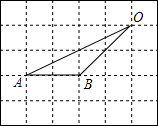 如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的正弦值是$\frac{\sqrt{5}}{5}$.
如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的正弦值是$\frac{\sqrt{5}}{5}$.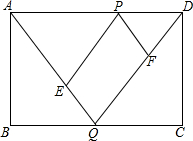 如图,矩形ABCD中,AB=2cm,BC=5cm,两动点P、Q分别同时从顶点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过P作PE∥DQ交AQ于点E,作PF∥AQ交DQ于点F.
如图,矩形ABCD中,AB=2cm,BC=5cm,两动点P、Q分别同时从顶点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过P作PE∥DQ交AQ于点E,作PF∥AQ交DQ于点F.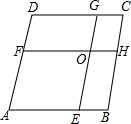 如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )
如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )