题目内容
13.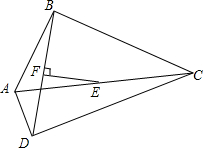 如图,在四边形ABCD中,E、F分别是AC、BD的中点,EF⊥BD,点F为垂足,∠ADC=90°.求∠ABC的度数.
如图,在四边形ABCD中,E、F分别是AC、BD的中点,EF⊥BD,点F为垂足,∠ADC=90°.求∠ABC的度数.
分析 根据题意可得BE=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AC,从而得到∠ABC=90°.
解答  证明:连接BE,DE,
证明:连接BE,DE,
∵EF⊥BD,点F是BD边的中点,
∴BE=DE,
∵∠ADC=90°,E是AC的中点,
∴DE=$\frac{1}{2}$AC,
∴BE=$\frac{1}{2}$AC,
∴∠ABC=90°.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
5.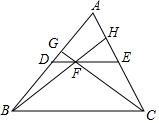 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )| A. | 1:10 | B. | 1:5 | C. | 3:10 | D. | 2:5 |
 如图,三个全等的小矩形沿“橫-竖-橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于672cm.
如图,三个全等的小矩形沿“橫-竖-橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于672cm.