题目内容
14.平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是5.分析 由点A、B的坐标可得到AB=2$\sqrt{2}$,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.
解答 解:
∵点A、B的坐标分别为(2,2)、B(4,0).
∴AB=2$\sqrt{2}$,
①若AC=AB,以A为圆心,AB为半径画弧与坐标轴有3个交点(含B点),即(0,0)、(4,0)、(0,4),
∵点(0,4)与直线AB共线,
∴满足△ABC是等腰三角形的C点有1个;
②若BC=AB,以B为圆心,BA为半径画弧与坐标轴有2个交点(A点除外),即满足△ABC是等腰三角形的C点有2个;
③若CA=CB,作AB的垂直平分线与坐标轴有两个交点,即满足△ABC是等腰三角形的C点有2个;
综上所述:点C在坐标轴上,△ABC是等腰三角形,符合条件的点C共有5个.
故答案为:5.
点评 本题主考查了等腰三角形的判定以及分类讨论思想的运用,分三种情况分别讨论,注意等腰三角形顶角的顶点在底边的垂直平分线上.

练习册系列答案
相关题目
5.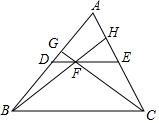 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )| A. | 1:10 | B. | 1:5 | C. | 3:10 | D. | 2:5 |
6.已知某圆锥的底面圆的半径r=2cm,将圆锥侧面展开得到一个圆心角θ=120°的扇形,则该圆锥的母线长l为( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
4. 如图,BD是⊙O的直径,点A、C在圆上,且CD=OB,则∠DAC等于( )
如图,BD是⊙O的直径,点A、C在圆上,且CD=OB,则∠DAC等于( )
 如图,BD是⊙O的直径,点A、C在圆上,且CD=OB,则∠DAC等于( )
如图,BD是⊙O的直径,点A、C在圆上,且CD=OB,则∠DAC等于( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |