题目内容
1.一段跑道长100米,甲、乙分别从A,B两端点同时相向出发,各以每秒6米和每秒4.5米的速度在跑道上来回往返练习跑步,问:在10分钟内(包括第10分钟).(1)甲和乙在途中迎面相遇多少次;
(2)甲在途中追上乙多少次;
(3)甲和乙在A,B两端点共相遇多少次.
分析 (1)根据速度和×时间=路程和,求得甲和乙在10分钟内跑的路程,再除以200得到一共跑了63个全程,再列出方程解方程即可求解;
(2)根据速度差×时间=路程差,再除以100即可求解;
(3)先求得600、900的最小公倍数,再用路程和除以最小公倍数,即可求解.
解答 解:(1)10分=600秒,
一共跑了(6+4.5)×600÷100=6300÷100=63个全程,
设甲和乙在途中迎面相遇x次,依题意有
2x=63+1,
解得x=32.
故甲和乙在途中迎面相遇32次.
(2)(6-4.5)×600÷100=900×100=9次.
故甲在途中追上乙9次.
(3)6×100=600,
4.5×200=900,
600、900的最小公倍数是1800,
一共跑了(6+4.5)×600=6300米,
6300÷1800=3…900.
故甲和乙在两端点A,B相遇3次.
点评 考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
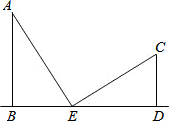 如图,两根电线杆AB,CD垂直于地面,AB=5cm,CD=3cm,现在施工人员在两根电线杆的底端之间(线段BD上)选一点E分别向电线杆顶端A,C拉钢索AE,CE,如果正好测得∠AEC=90°,且AE=CE.那么BE的长为多少?
如图,两根电线杆AB,CD垂直于地面,AB=5cm,CD=3cm,现在施工人员在两根电线杆的底端之间(线段BD上)选一点E分别向电线杆顶端A,C拉钢索AE,CE,如果正好测得∠AEC=90°,且AE=CE.那么BE的长为多少? 如图,在△ABC中,AB=BC,∠ABC=90°,点E,F分别在AB,AC上,且AE=EF,点O,M分别为AF,CE的中点.求证:OB=$\sqrt{2}$OM.
如图,在△ABC中,AB=BC,∠ABC=90°,点E,F分别在AB,AC上,且AE=EF,点O,M分别为AF,CE的中点.求证:OB=$\sqrt{2}$OM. 如图,在?ABCD中,点E,F分别是AB,CD的中点,且CA=CB,连接AF,CE.求证:四边形AECF是矩形.
如图,在?ABCD中,点E,F分别是AB,CD的中点,且CA=CB,连接AF,CE.求证:四边形AECF是矩形.