题目内容
19. 如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )
如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )| A. | 40° | B. | 45° | C. | 73° | D. | 85° |
分析 先根据三角形内角和定理求出∠BAC的度数,再根据角平分线的性质得出∠BAD的度数,由三角形内角和定理即可得出结论.
解答 解:∵在△ABC中,∠B=67°,∠C=33°,
∴∠BAC=180°-67°-33°=80°,
∵AD是△ABC的角平分线,
∴∠BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×80°=40°,
∴∠ADB=180°-∠B-∠BAD=180°-67°-40°=73°.
故选C.
点评 本题考查的是三角形的角平分线:三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.也考查了三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
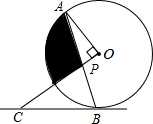 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB. 如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由.
如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由.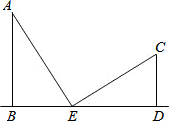 如图,两根电线杆AB,CD垂直于地面,AB=5cm,CD=3cm,现在施工人员在两根电线杆的底端之间(线段BD上)选一点E分别向电线杆顶端A,C拉钢索AE,CE,如果正好测得∠AEC=90°,且AE=CE.那么BE的长为多少?
如图,两根电线杆AB,CD垂直于地面,AB=5cm,CD=3cm,现在施工人员在两根电线杆的底端之间(线段BD上)选一点E分别向电线杆顶端A,C拉钢索AE,CE,如果正好测得∠AEC=90°,且AE=CE.那么BE的长为多少?