题目内容
4.n是整数,式子$\frac{1}{8}$[1-(-1)n](n2-1)计算的结果( )| A. | 是0 | B. | 总是奇数 | ||
| C. | 总是偶数 | D. | 可能是奇数也可能是偶数 |
分析 根据题意,可以利用分类讨论的数学思想探索式子$\frac{1}{8}$[1-(-1)n](n2-1)计算的结果等于什么,从而可以得到哪个选项是正确的.
解答 解:当n是偶数时,
$\frac{1}{8}$[1-(-1)n](n2-1)=$\frac{1}{8}$[1-1](n2-1)=0,
当n是奇数时,
$\frac{1}{8}$[1-(-1)n](n2-1)=$\frac{1}{8}$×(1+1)(n+1)(n-1)=$\frac{(n+1)(n-1)}{4}$,
设n=2k-1(k为整数),
则$\frac{(n+1)(n-1)}{4}$=$\frac{(2k-1+1)(2k-1-1)}{4}$=k(k-1),
∵0或k(k-1)(k为整数)都是偶数,
故选C.
点评 本题考查因式分解的应用,解题的关键是明确题意,利用分类讨论的数学思想解答问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
| A. | AB∥DC,AD=BC | B. | AB=DC,AD=BC | C. | AO=CO,BO=DO | D. | AB∥DC,AD∥BC |
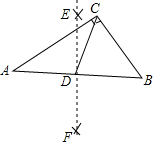 如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是5.
如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是5.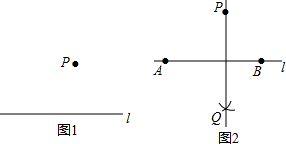 下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
 将矩形ABCD折叠使点A,C重合,折痕交BC于点E,交AD于点F,可以得到四边形AECF是一个菱形,若AB=4,BC=8,求菱形AECF的面积.
将矩形ABCD折叠使点A,C重合,折痕交BC于点E,交AD于点F,可以得到四边形AECF是一个菱形,若AB=4,BC=8,求菱形AECF的面积.