题目内容
已知线段AB,在直线AB上有一点O,C为AO中点,D为BO的中点,若AB的长度为12CM,求CD的长度.
考点:两点间的距离
专题:计算题
分析:分类讨论:当点O在线段AB上,如图1,根据线段中点的定义得到CO=
AO,DO=
BO,则CD=CO+DO=
AB=6cm;当点O在线段AB的延长线上,如图2,
同样得到CO=
AO,DO=
BO,则CD=CO-DO=
AB=6cm;当点O在线段BA的延长线上,同理可得CD=6cm.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
同样得到CO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:当点O在线段AB上,如图1,
∵C为AO中点,D为BO的中点,
∴CO=
AO,DO=
BO,
∴CO+DO=
(AO+BO),
∴CD=
×12cm=6cm;
当点O在线段AB的延长线上,如图2,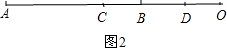
∵C为AO中点,D为BO的中点,
∴CO=
AO,DO=
BO,
∴CO-DO=
(AO-BO),
∴CD=
×12cm=6cm;
当点O在线段BA的延长线上,同理可得CD=6cm,
综上所述,CD的长为6cm.

∵C为AO中点,D为BO的中点,
∴CO=
| 1 |
| 2 |
| 1 |
| 2 |
∴CO+DO=
| 1 |
| 2 |
∴CD=
| 1 |
| 2 |
当点O在线段AB的延长线上,如图2,

∵C为AO中点,D为BO的中点,
∴CO=
| 1 |
| 2 |
| 1 |
| 2 |
∴CO-DO=
| 1 |
| 2 |
∴CD=
| 1 |
| 2 |
当点O在线段BA的延长线上,同理可得CD=6cm,
综上所述,CD的长为6cm.
点评:本题考查了两点的距离:连接两点间的线段的长度叫两点间的距离.注意强调最后的两个字“长度”,也就是说,距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
下列命题是真命题的是( )
| A、4是2的平方根 |
| B、2是4的算术平方根 |
| C、0的算术平方根不存在 |
| D、-1是-1的算术平方根 |
下列四个函数中,y随x的增大而减小的是( )
| A、y=3x | ||
| B、y=x2(x<0) | ||
| C、y=x+3 | ||
D、y=
|
 用6m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积为1.44m2?(设窗框宽为xm )
用6m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积为1.44m2?(设窗框宽为xm )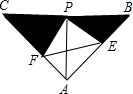 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF=
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF=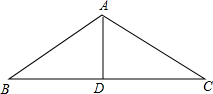 如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数.
如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数. 已知AB是⊙O的直径,在OA上取一点M,作MC、MD与⊙O分别交于C、D两点,且∠BMC=∠BMD.求证:MC=MD.
已知AB是⊙O的直径,在OA上取一点M,作MC、MD与⊙O分别交于C、D两点,且∠BMC=∠BMD.求证:MC=MD. 如图,已知点C为BD的中点,AB∥DE,∠1=∠2.求证:AF=EG.
如图,已知点C为BD的中点,AB∥DE,∠1=∠2.求证:AF=EG. 如图,AC是⊙O的直径,OE⊥AB,OF⊥AD,E,F为垂足,OE=OF,AC2=AD•AB,求证:BC是⊙O的切线.
如图,AC是⊙O的直径,OE⊥AB,OF⊥AD,E,F为垂足,OE=OF,AC2=AD•AB,求证:BC是⊙O的切线.