Question

19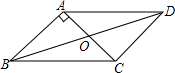．已知：如图，在?ABCD中，对角线AC，BD交于点O，AB⊥AC，AB=2，BC=$\sqrt{7}$．
（1）求平行四边形ABCD的面积S_?ABCD；
（2）求对角线BD的长．

Answer 1

分析 （1）先根据勾股定理求出AC的长，再根据S_?ABCD=2S_△ABC即可得出结论；
（2）根据AC的长得出OA的长，由勾股定理求出OB的长，进而可得出结论．

解答 解：（1）∵AB⊥AC，AB=2，BC=$\sqrt{7}$，
∴AC=$\sqrt{{BC}^{2}-{AB}^{2}}$=$\sqrt{{（\sqrt{7}）}^{2}-{2}^{2}}$=$\sqrt{3}$，
∴S_?ABCD=2S_△ABC=2×$\frac{1}{2}$×2×$\sqrt{3}$=2$\sqrt{3}$；

（2）∵AC=$\sqrt{3}$，
∴OA=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$，
∴OB=$\sqrt{{AB}^{2}+{OA}^{2}}$=$\sqrt{{2}^{2}+{（\frac{\sqrt{3}}{2}）}^{2}}$=$\frac{\sqrt{19}}{2}$，
∴BD=2OB=$\sqrt{19}$．

点评 本题考查的是平行四边形的性质，熟知平行四边形的对角线互相平分是解答此题的关键．