题目内容
7．若2x2-5x+2＜0，则$\sqrt{4{x}^{2}-4x+1}$+2|x-2|等于（ ）| A． | 4x-5 | B． | -3 | C． | 3 | D． | 5-4x |
分析 根据2x2-5x+2＜0，可以确定x的取值范围，从而得到$\sqrt{4{x}^{2}-4x+1}$+2|x-2|的值．
解答 解：∵2x2-5x+2＜0，
∴（2x-1）（x-2）＜0，
解得，$\frac{1}{2}＜x＜2$，
∴$\sqrt{4{x}^{2}-4x+1}$+2|x-2|
=$\sqrt{（2x-1）^{2}}+2（2-x）$
=2x-1+4-2x
=3，
故选C．
点评 本题考查二次根式的混合运算，解题的关键是明确二次根式的混合运算的计算方法．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
17．已知二次函数y=（x-h）2+1（h为常数），在自变量x的值满足1≤x≤4的情况下，与其对应的函数值y的最小值为5，则h的值为（ ）
| A． | 1或-6 | B． | -1或6 | C． | 1或-4 | D． | 1或4 |
有理数a、b在数轴上的位置如图所示
15．在线段、等腰梯形、平行四边形、矩形、菱形、正方形、等边三角形中，既是轴对称图形又是中心对称图形的有（ ）
| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
12．
如图，四边形ABCD是⊙O的内接四边形，∠B=135°，则∠AOC的度数（ ）
如图，四边形ABCD是⊙O的内接四边形，∠B=135°，则∠AOC的度数（ ）| A． | 60° | B． | 70° | C． | 90° | D． | 180° |
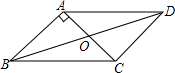已知：如图，在?ABCD中，对角线AC，BD交于点O，AB⊥AC，AB=2，BC=$\sqrt{7}$．
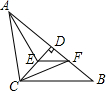已知等腰直角三角形ABC中，CD是斜边AB上的高，AE平分∠CAB交CD于E，在DB上取点F，使DF=DE，求证：CF平分∠DCB．