题目内容
4.已知:在△ABC中,AB=AC,AD⊥BC,垂足为点D,E在CB的延长线上,且BE=2BD,连接AE,F是AC的中点,G是AE的中点,连接BG、BF.(1)如图1,求证:四边形AGBF是平行四边形.
(2)如图2,连接GF、DF,GF与AB相交于点H,若GF=AB,在不添加任何辅助线的情况下,请直接写出图2中所有的等边三角形.

分析 (1)由AB=AC,AD⊥BC,根据三线合一的知识,可得BC=2BD,又由BE=2BD,可得B是EC的中点,又由F是AC的中点,G是AE的中点,根据三角形中位线的性质,即可得BG∥AC,BF∥AE,即可判定:四边形AGBF是平行四边形.
(2)易证得四边形BGFC是平行四边形,由GF=AB,可判定△ABC是等边三角形,继而可得△AHF,△CDF,△GHB是等边三角形.
解答 (1)证明:∵AB=AC,AD⊥BC,
∴BC=2BD,
∵BE=2BD,
∴BC=BE,
∵F是AC的中点,G是AE的中点,
∴BG∥AC,BF∥AE,
∴四边形AGBF是平行四边形.
(2)∵F是AC的中点,G是AE的中点,
∴GF∥BC,
∵BG∥AC,
∴四边形BGFC是平行四边形,
∴GF=BC,
∵GF=AB,AB=AC,
∴AB=AC=BC,
即△ABC是等边三角形,
∵GF∥BC,DF∥AB,BG∥AC,
∴△AHF∽△ABC,△CDF∽△CBA,△GBH∽△FAH,
∴△AHF,△CDF,△GHB是等边三角形,
综上可得:图2中等边三角形有:△ABC,△AHF,△CDF,△GHB.
点评 此题考查了平行四边形的性质以及等边三角形的判定与性质.注意证得B是EC的中点,根据三角形中位线的性质求解是关键.

练习册系列答案
相关题目
12.不透明的布袋中有2个白球,3个黑球,除颜色外其他都相同,从中随机摸出一个球,恰好为黑球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
19.下列运算中,正确的是( )
| A. | x+x2=x3 | B. | 2x3÷x2=x | C. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{8}$ | D. | (a+4)(a+3)=a2+12 |
9. 如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB的大小是( )
如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB的大小是( )
 如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB的大小是( )
如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB的大小是( )| A. | 50° | B. | 40° | C. | 25° | D. | 100° |
16.下列格式计算正确的是( )
| A. | 2-1=-2 | B. | $\sqrt{8}-\sqrt{2}$=$\sqrt{6}$ | C. | x2•x3=x6 | D. | (-4x4)÷(2x2)=-2x2 |
14.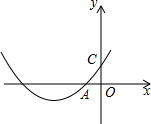 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
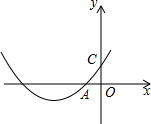 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )| A. | ac+1=b | B. | ab+1=c | C. | bc+1=a | D. | 以上都不是 |
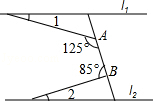 如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=30°.
如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=30°.