题目内容
3.在直角坐标系中,A,B,C,D四点在坐标轴上,如图所示满足AO=BO,BC⊥AD,D(1,0).(1)求C点坐标;
(2)点M、N分别是BC,AD的中点,连接OM,ON,判断OM,ON的关系;
(3)在(2)的条件下,连AM,BN,取BN的中点P,连OP.当C、D分别以相同的速度沿着y轴、x轴向原点O运动过程中,求证:∠MAC+∠POA为定值.

分析 (1)由ASA证明△OBC≌△OAD,得出对应边相等,即可得出结果;
(2)由全等三角形的性质得出BC=AD,∠OBC=∠OAN,由直角三角形斜边上的中线性质得出OM=$\frac{1}{2}$BC=BM,ON=$\frac{1}{2}$AD=AN,即可得出结论;
(3)在x轴上截取OF=OB=OA,连接FN,由(2)得:OM=BM,ON=AN,得出∠MOB=∠MBO,∠NAO=∠NOA,因此∠MOB=∠NOA,证出∠MON=90°,由旋转的性质得出∠MAC=∠NFO,证明OP是△BFN的中位线,由三角形中位线定理得出OP∥FN,由平行线的性质得出∠NFO=∠POB,即可得出结论.
解答 (1)解:∵BC⊥AD,D(1,0),
∴∠OBC+∠ADO=90°,OD=1,
∵∠AOD=∠BOC=90°,
∴∠OAD+∠ADO=90°,
∴∠OBC=∠OAD,
在△OBC和△OAD中,$\left\{\begin{array}{l}{∠BOC=∠AOD}&{\;}\\{OB=OA}&{\;}\\{∠OBC=∠OAD}&{\;}\end{array}\right.$,
∴△OBC≌△OAD(ASA),
∴OC=OD=1,
∴C点坐标为(0,1);
(2)解:OM=ON;理由如下:
由(1)得:△OBC≌△OAD,
∴BC=AD,∠OBC=∠OAN,
∵∠BOC=∠AOD=90°,点M、N分别是BC,AD的中点,
∴OM=$\frac{1}{2}$BC=BM,ON=$\frac{1}{2}$AD=AN,
∴OM=ON;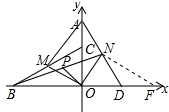
(3)证明:在x轴上截取OF=OB=OA,连接FN,如图所示:
由(2)得:OM=BM,ON=AN,
∴∠MOB=∠MBO,∠NAO=∠NOA,
∴∠MOB=∠NOA,
∵∠BOM+∠AOM=90°,
∴∠AOM+∠NOA=90°,
即∠MON=90°,
把△AOM绕点O顺时针旋转90°与△FON重合,
∴∠MAC=∠NFO,
∵P是BN的中点,OF=OB,
∴OP是△BFN的中位线,
∴OP∥FN,
∴∠NFO=∠POB,
∴∠MAC=∠POB,
∵∠POB+∠POA=90°,
∴∠MAC+∠POA=90°;
即∠MAC+∠POA为定值.
点评 本题考查了全等三角形的判定与性质、坐标与图形性质、直角三角形斜边上的中线性质、等腰三角形的性质、旋转的性质等知识;本题综合性强,有一定难度,特别是(3)中,需要通过作辅助线运用旋转的性质和三角形中位线定理才能得出结论.


| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.
如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.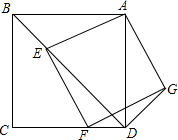 如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG,
如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG, 画一个正方形,使它的面积是图中正方形面积的4倍.
画一个正方形,使它的面积是图中正方形面积的4倍.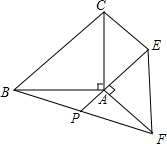 如图,等腰直角△ABC和等腰直角△AEF,∠BAC=∠EAF=90°,连结CE、BF,延长EA交BF于P,当点P为BF的中点时,求$\frac{CE}{AP}$的值.
如图,等腰直角△ABC和等腰直角△AEF,∠BAC=∠EAF=90°,连结CE、BF,延长EA交BF于P,当点P为BF的中点时,求$\frac{CE}{AP}$的值.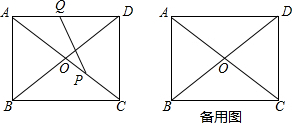 如图,在矩形ABCD中,AD=4,DC=3,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿C→O→B运动.到点B停止,点Q沿A→D→C运动,到点C停止.连接AP、AQ、PQ,设△APQ的面积为y(cm2)(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).
如图,在矩形ABCD中,AD=4,DC=3,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿C→O→B运动.到点B停止,点Q沿A→D→C运动,到点C停止.连接AP、AQ、PQ,设△APQ的面积为y(cm2)(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).