题目内容
16.(1)计算:$\frac{{a}^{2}-{b}^{2}}{a-b}$÷$\frac{{a}^{2}+ab}{2a-2b}$(2)解方程:$\frac{1-x}{x-4}$-2=$\frac{3}{4-x}$.
分析 (1)先把分子分母因式分解,再把除法运算化为乘法运算,然后约分即可;
(2)先把分式方程化为整式方程得1-x-2(x-4)=-3,再解整式方程,然后进行检验确定原方程的解.
解答 解:(1)原式=$\frac{(a+b)(a-b)}{a-b}$•$\frac{2(a+b)}{a(a+b)}$
=$\frac{2a-2b}{a}$;
(2)去分母得1-x-2(x-4)=-3,
解得 x=4,
经检验,x=4是增根,
所以原方程无解.
点评 本题考查了解分式方程:熟练掌握解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.也考查了分式的乘除法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
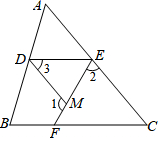 如图,在三角形ABC中,D,E,F三点分别在AB,AC,BC上,过点D的直线与线段EF的交点为点M,已知2∠1-∠2=150°,2∠2-∠1=30°.
如图,在三角形ABC中,D,E,F三点分别在AB,AC,BC上,过点D的直线与线段EF的交点为点M,已知2∠1-∠2=150°,2∠2-∠1=30°.
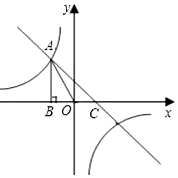 如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,2),过点A作AB⊥x轴于点B,连结AO.
如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,2),过点A作AB⊥x轴于点B,连结AO.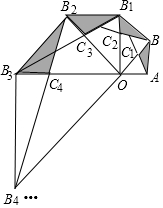 如图,△OAB中,∠OAB=90°,OA=AB=1.以OB为直角边向外作等腰直角三角形OBB1,以OB1为直角边向外作等腰直角三角形OB1B2,以OB2为直角边向外作等腰直角三角形OB2B3,…,连接AB1,BB2,B1B3,…,分别与OB,OB1,OB2,…交于点C1,C2,C3,…,按此规律继续下去,△ABC1的面积记为S1,△BB1C2的面积记为S2,△B1B2C3的面积记为S3,…,则S2017=$\frac{1}{3}$×22015..
如图,△OAB中,∠OAB=90°,OA=AB=1.以OB为直角边向外作等腰直角三角形OBB1,以OB1为直角边向外作等腰直角三角形OB1B2,以OB2为直角边向外作等腰直角三角形OB2B3,…,连接AB1,BB2,B1B3,…,分别与OB,OB1,OB2,…交于点C1,C2,C3,…,按此规律继续下去,△ABC1的面积记为S1,△BB1C2的面积记为S2,△B1B2C3的面积记为S3,…,则S2017=$\frac{1}{3}$×22015..