题目内容
7.(1)计算:$\frac{{a}^{2}}{a-1}$-a-1;(2)化简:$\frac{{x}^{2}+1}{{x}^{2}-1}$-$\frac{x-2}{x-1}$÷$\frac{x-2}{x}$,并在-3≤x≤2中选取一个你喜欢的整数x的值代入求值.
分析 根据分式的运算法则即可求出答案.
解答 解:(1)原式=$\frac{{a}^{2}}{a-1}$-$\frac{(a+1)(a-1)}{a-1}$
=$\frac{1}{a-1}$
(2)原式=$\frac{{x}^{2}+1}{{x}^{2}-1}$-$\frac{x-2}{x-1}$×$\frac{x}{x-2}$
=$\frac{{x}^{2}+1}{(x+1)(x-1)}$-$\frac{x(x+1)}{(x-1)(x+1)}$
=-$\frac{1}{x+1}$
∵$\left\{\begin{array}{l}{{x}^{2}-1≠0}\\{x-1≠0}\\{x≠0}\\{x-2≠0}\end{array}\right.$
解得:x≠±1且x≠0且x≠2
∴令x=3代入得,原式=-$\frac{1}{4}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列说法正确的是( )
| A. | -4是-16的平方根 | B. | 4是(-4)2的平方根 | C. | (-6)2的平方根是-6 | D. | ±$\sqrt{64}$的平方根是±8 |
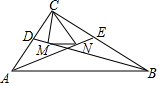 在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN=2.
在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN=2.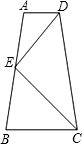 如图,已知梯形ABCD中,AD∥BC,E为AB中点,DE⊥EC.
如图,已知梯形ABCD中,AD∥BC,E为AB中点,DE⊥EC.