题目内容
8.已知四边形ABCD是菱形,对角线AC、BD交于点O.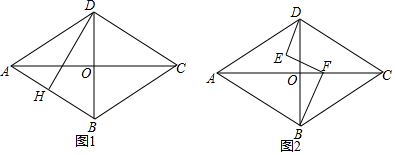
(1)如图1,若AC=8,BD=6,DH⊥AB于H.求DH的长.
(2)如图2,F是AC上一点,分别过点B,D作过F点的直线的垂线,垂足分别为F和E,若DE=4,EF=3,求BD的长.
分析 (1)利用面积法S菱形ABCD=$\frac{1}{2}$•AC•BD=AB•DH,即可解决问题;
(2)如图2中,作BH⊥DE交DE的延长线于H,连接DF,则四边形EFBH是矩形.在Rt△DHB中,求出DH、BH即可解决问题;
解答 解:(1)如图1中,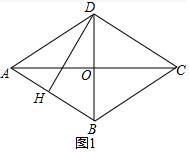
∵四边形ABCD是菱形,
∴OA=OC=4,OD=OB=3,AC⊥BD,
∴∠AOB=90°,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵S菱形ABCD=$\frac{1}{2}$•AC•BD=AB•DH,
∴DH=$\frac{24}{5}$.
(2)如图2中,作BH⊥DE交DE的延长线于H,连接DF,则四边形EFBH是矩形.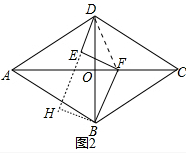
在Rt△EDF中,DF=$\sqrt{D{E}^{2}+E{F}^{2}}$=5,
易知BF=DF=5,
∴EH=BF=5,BH=EF=3,
在Rt△BDH中,BD=$\sqrt{D{H}^{2}+B{H}^{2}}$=$\sqrt{{9}^{2}+{3}^{2}}$=3$\sqrt{10}$.
点评 本题考查菱形的性质、勾股定理、矩形的判定和性质等知识,解题的关键是学会利用面积法求高,学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
3.已知2x-y=3,用含x的代数式表示y,正确的是( )
| A. | y=3-2x | B. | y=2x-3 | C. | y=2x+3 | D. | x=$\frac{y+3}{2}$ |
20.对于一次函数y=-2x+4,下列结论错误的是( )
| A. | 若两点 A(x1,y1),B(x2,y2)在该函数图象上,且 x1<x2,则 y1>y2 | |
| B. | 函数的图象不经过第三象限 | |
| C. | 函数的图象向下平移4个单位长度得y=-2x的图象 | |
| D. | 函数的图象与x轴的交点坐标是(0,4) |
17.下列说法正确的是( )
| A. | -4是-16的平方根 | B. | 4是(-4)2的平方根 | C. | (-6)2的平方根是-6 | D. | ±$\sqrt{64}$的平方根是±8 |
10.在一年一次的安全知识考试中,其中有10道多项选择题,每题分值相同,每题必答.下面不完整的表格记录了四位同学的得分情况.
(1)分析表格数据,直接填空:答对一道全部选项的题,得5分,答出一道部分选项正确且未选错误项的题,得2分,选出一道有错误选项的题,得-1分;
(2)英英同学有1题答对部分选项且未选错误项,总得分为35分,求英英答对全部选项的题数.
| 学生姓名 | 答对全部选项的题数 | 答对部分选项且未选错误项的题数 | 有错误选项的题数 | 得分 |
| 伍伍 | 10 | 0 | 0 | 50 |
| 佳佳 | 9 | 0 | 1 | 44 |
| 刚刚 | 6 | 2 | 2 | 32 |
| 英英 | 1 | 35 |
(2)英英同学有1题答对部分选项且未选错误项,总得分为35分,求英英答对全部选项的题数.
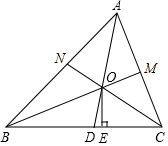 如图,在△ABC中,三个内角的平分线AD、BM、CN交于点O,OE⊥BC于点E.
如图,在△ABC中,三个内角的平分线AD、BM、CN交于点O,OE⊥BC于点E.