题目内容
11.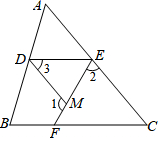 如图,在三角形ABC中,D,E,F三点分别在AB,AC,BC上,过点D的直线与线段EF的交点为点M,已知2∠1-∠2=150°,2∠2-∠1=30°.
如图,在三角形ABC中,D,E,F三点分别在AB,AC,BC上,过点D的直线与线段EF的交点为点M,已知2∠1-∠2=150°,2∠2-∠1=30°.(1)求证:DM∥AC;
(2)若DE∥BC,∠C=50°,求∠3的度数.
分析 (1)将2∠1-∠2=150°、2∠2-∠1=30°二者相加即可得出∠1+∠2=180°,根据邻补角可得出∠1+∠DME=180°,进而可得出∠2=∠DME,再根据“内错角相等,两直线平行”即可证出DM∥AC;
(2)由DM∥AC可得出∠3=∠AED,根据DE∥BC可得出∠AED=∠C,通过替换结合∠C的度数即可求出∠3的度数.
解答 (1)证明:∵2∠1-∠2=150°,2∠2-∠1=30°,
∴∠1+∠2=180°.
∵∠1+∠DME=180°,
∴∠2=∠DME.
∴DM∥AC.
(2)解:∵DM∥AC,
∴∠3=∠AED.
∵DE∥BC,
∴∠AED=∠C,
∴∠3=∠C.
∵∠C=50°,
∴∠3=50°.
点评 本题考查了平行线的判定与性质以及邻补角,解题的关键是:(1)通过角的计算找出∠2=∠DME;(2)根据平行线的性质找出∠3=∠AED=∠C.

练习册系列答案
相关题目
3.已知2x-y=3,用含x的代数式表示y,正确的是( )
| A. | y=3-2x | B. | y=2x-3 | C. | y=2x+3 | D. | x=$\frac{y+3}{2}$ |
20.对于一次函数y=-2x+4,下列结论错误的是( )
| A. | 若两点 A(x1,y1),B(x2,y2)在该函数图象上,且 x1<x2,则 y1>y2 | |
| B. | 函数的图象不经过第三象限 | |
| C. | 函数的图象向下平移4个单位长度得y=-2x的图象 | |
| D. | 函数的图象与x轴的交点坐标是(0,4) |
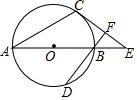 如图,AB是⊙O的直径,AC是⊙O的弦,E是AB延长线上的点,BF⊥EC于F交⊙O于D,∠EBF=2∠EAC.
如图,AB是⊙O的直径,AC是⊙O的弦,E是AB延长线上的点,BF⊥EC于F交⊙O于D,∠EBF=2∠EAC.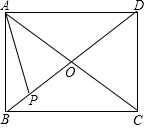 在矩形ABCD中,AB=6,BC=8,∠DAO=∠PAO,求AP的长.
在矩形ABCD中,AB=6,BC=8,∠DAO=∠PAO,求AP的长.