题目内容
9. 小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,并拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.求旗杆AB的高度和小明后退的距离EC.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1m)
小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,并拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.求旗杆AB的高度和小明后退的距离EC.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1m)
分析 设绳子AC的长为x米;由三角函数得出AB,过D作DF⊥AB于F,根据△ADF是等腰直角三角形,得出方程,解方程即可.
解答 解:设绳子AC的长为x米;
在△ABC中,AB=AC•sin60°,
过D作DF⊥AB于F,如图:
∵∠ADF=45°,
∴△ADF是等腰直角三角形,
∴AF=DF=x•sin45°,
∵AB-AF=BF=1.6,则x•sin60°-x•sin45°=1.6,
解得:x=10,
∴AB=10×sin60°≈8.7(m),
EC=EB-CB=x•cos45°-x•cos60°=10×$\frac{\sqrt{2}}{2}$-10×$\frac{1}{2}$≈2.1(m)
答:旗杆AB的高度为8.7m,小明后退的距离为2.1m.
点评 本题考查了解直角三角形的应用-仰角、等腰直角三角形的判定与性质;熟练掌握三角函数,根据题意得出方程是解决问题的关键,本题难度适中.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
4.函数$y=\frac{{\sqrt{x+1}}}{x}$中自变量x的取值范围是( )
| A. | x≥-1 | B. | x≤-1 | C. | x≥-1且x≠0 | D. | x≠0 |
1.下列说法正确的是( )
| A. | 了解我国青年人喜欢的电视节目应作全面调查 | |
| B. | “购买1张彩票就中奖”是不可能事件 | |
| C. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 | |
| D. | 甲、乙两组数据,若${{S}_{甲}}^{2}$>${{S}_{乙}}^{2}$,则乙组数据离散程度大 |
 在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E.
在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E.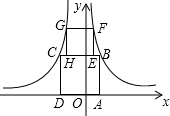 如图,四边形ABCD与EFGH均为正方形,点B、F在函数y=$\frac{1}{x}$(x>0)的图象上,点G、C在函数y=-$\frac{3}{x}$(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标$\sqrt{5}$+1.
如图,四边形ABCD与EFGH均为正方形,点B、F在函数y=$\frac{1}{x}$(x>0)的图象上,点G、C在函数y=-$\frac{3}{x}$(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标$\sqrt{5}$+1.