题目内容
17.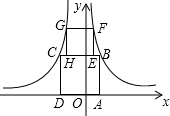 如图,四边形ABCD与EFGH均为正方形,点B、F在函数y=$\frac{1}{x}$(x>0)的图象上,点G、C在函数y=-$\frac{3}{x}$(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标$\sqrt{5}$+1.
如图,四边形ABCD与EFGH均为正方形,点B、F在函数y=$\frac{1}{x}$(x>0)的图象上,点G、C在函数y=-$\frac{3}{x}$(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标$\sqrt{5}$+1.
分析 设线段AB的长度为a,线段EF的长度为b(a>0,b>0),利用反比例函数图象上点的坐标特征找出点B、C、F、G的坐标,再根据正方形的性质找出线段相等,从而分别找出关于a和关于b的一元二次方程,解方程即可得出a、b的值,从而得出结论.
解答 解:设线段AB的长度为a,线段EF的长度为b(a>0,b>0),
令y=$\frac{1}{x}$(x>0)中y=a,则x=$\frac{1}{a}$,
即点B的坐标为($\frac{1}{a}$,a);
令y=-$\frac{3}{x}$(x<0)中y=a,则x=-$\frac{3}{a}$,
即点C的坐标为(-$\frac{3}{a}$,a).
∵四边形ABCD为正方形,
∴$\frac{1}{a}$-(-$\frac{3}{a}$)=a,
解得:a=2,或a=-2(舍去).
令y=$\frac{1}{x}$(x>0)中y=2+b,则x=$\frac{1}{2+b}$,
即点F的坐标为($\frac{1}{2+b}$,2+b);
令y=-$\frac{3}{x}$(x<0)中y=2+b,则x=-$\frac{3}{2+b}$,
即点G的坐标为(-$\frac{3}{2+b}$,2+b).
∵四边形EFGH为正方形,
∴$\frac{1}{2+b}$+(-$\frac{3}{2+b}$)=b,即b2+2b-4=0,
解得:b=$\sqrt{5}$-1,或b=-$\sqrt{5}$-1(舍去).
∴a+b=2+$\sqrt{5}$-1=$\sqrt{5}$+1.
故答案为:$\sqrt{5}$+1.
点评 本题考查了反比例函数图象上点的坐标特征以及正方形的性质,解题的关键是求出a、b值.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数图象上点的坐标特征找出点的坐标,再结合正方形的性质分别找出关于正方形边长的一元二次方程是关键.

| 月用水量 | 频数 |
| 0≤x<0.5 | 1 |
| 0.5≤x<1 | 2 |
| 1≤x<1.5 | 3 |
| 1.5≤x<2 | 4 |
| 2≤x<2.5 | 3 |
| 2.5≤x<3 | 3 |
| 3≤x<3.5 | 2 |
| 3.5≤x<4 | 1 |
| 4≤x<4.5 | 1 |
| A. | 0.15 | B. | 0.3 | C. | 0.8 | D. | 0.9 |
| A. | |-3| | B. | -$\sqrt{3}$ | C. | -$\frac{1}{3}$ | D. | -π |
| A. | $\sqrt{7}$ | B. | 6 | C. | -$\frac{1}{3}$ | D. | 2.5 |
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | 3 |
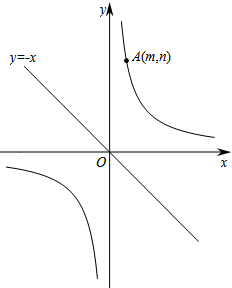 如图,已知直线y=-x和双曲线$y=\frac{k}{x}$(k>0),点A(m,n)(m>0)在双曲线$y=\frac{k}{x}$上.
如图,已知直线y=-x和双曲线$y=\frac{k}{x}$(k>0),点A(m,n)(m>0)在双曲线$y=\frac{k}{x}$上. 如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4). 小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,并拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.求旗杆AB的高度和小明后退的距离EC.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1m)
小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,并拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.求旗杆AB的高度和小明后退的距离EC.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1m)