��Ŀ����
ij��ҵ��Ͷ��10��Ԫ����A��B���ֲ�Ʒ������ҵ��Ϣ�������г����з��֣�
��Ϣһ���������Ͷ��A�ֲ�Ʒ������������yA����Ԫ����Ͷ�ʽ��x����Ԫ��֮�����������������ϵ��yA=kx�����ҵ�Ͷ��5��Ԫʱ���ɻ�����2��Ԫ��
��Ϣ�����������Ͷ��B�ֲ�Ʒ������������yB����Ԫ����Ͷ�ʽ��x����Ԫ��֮����ڶ��κ�����ϵ��yB=ax2+bx�����ҵ�Ͷ��2��Ԫʱ���ɻ�����2.4��Ԫ����Ͷ��4��Ԫʱ���ɻ�����3.2��Ԫ��
��1����ֱ������������������������ʽ����κ�������ʽ��
��2���������һ���ܻ����������Ͷ�ʷ�������������˷����ܻ�õ��������
��3���������Ͷ�ʷ���ʹ����ҵ��Ҫ��õ�������5��Ԫ��
��Ϣһ���������Ͷ��A�ֲ�Ʒ������������yA����Ԫ����Ͷ�ʽ��x����Ԫ��֮�����������������ϵ��yA=kx�����ҵ�Ͷ��5��Ԫʱ���ɻ�����2��Ԫ��
��Ϣ�����������Ͷ��B�ֲ�Ʒ������������yB����Ԫ����Ͷ�ʽ��x����Ԫ��֮����ڶ��κ�����ϵ��yB=ax2+bx�����ҵ�Ͷ��2��Ԫʱ���ɻ�����2.4��Ԫ����Ͷ��4��Ԫʱ���ɻ�����3.2��Ԫ��
��1����ֱ������������������������ʽ����κ�������ʽ��
��2���������һ���ܻ����������Ͷ�ʷ�������������˷����ܻ�õ��������
��3���������Ͷ�ʷ���ʹ����ҵ��Ҫ��õ�������5��Ԫ��
���㣺���κ�����Ӧ��
ר�⣺�����ۺ���
��������1�����ô���ϵ��������������������ʽ������κ�������ʽ��ɣ�
��2����Ͷ��B��Ʒx��Ԫ����Ͷ��A��Ʒ��10-x����Ԫ��Ȼ��д���������ʽ���ٸ��ݶ��κ�������ֵ������
��3����y=5��������������ϵʽ�����ʱ��x��ֵ��Ȼ����ݶ��κ��������ʽ�ɣ�
��2����Ͷ��B��Ʒx��Ԫ����Ͷ��A��Ʒ��10-x����Ԫ��Ȼ��д���������ʽ���ٸ��ݶ��κ�������ֵ������
��3����y=5��������������ϵʽ�����ʱ��x��ֵ��Ȼ����ݶ��κ��������ʽ�ɣ�
����⣺��1����yA=kx����Ͷ��5��Ԫʱ���ɻ�����2��
��5k=2��
��k=
��
���ԣ�������ϵʽΪyA=
x��
��yB=ax2+bx��Ͷ��2��Ԫʱ���ɻ�����2.4��Ԫ����Ͷ��4��Ԫʱ���ɻ�����3.2��Ԫ��
��
��
���
��
���ԣ�yB=-
x2+
x��
��2����Ͷ��B��Ʒx��Ԫ����Ͷ��A��Ʒ��10-x����Ԫ��
����y=-
x2+
x+
��10-x��=-
x2+
x+4=-
��x2-6x+9��+
+4=-
��x-3��2+5.8��
��y=-
��x-3��2+5.8��
���ԣ���Ͷ��B��Ʒ3��Ԫʱ���ܻ�õ��������
��ʱͶ��A��Ʒ7��Ԫ��B��Ʒ3��Ԫ��������������5.8��Ԫ��
��3��y=5ʱ��-
��x-3��2+5.8=5��
�����ã�x-3��2=4��
����x-3=2��x-3=-2��
���ԣ�x1=5��x2=1��
��a=-
��0��
��Ͷ��B��Ʒ1��5��Ԫʱ����õ�������5��Ԫ��
��5k=2��
��k=
| 2 |
| 5 |
���ԣ�������ϵʽΪyA=
| 2 |
| 5 |
��yB=ax2+bx��Ͷ��2��Ԫʱ���ɻ�����2.4��Ԫ����Ͷ��4��Ԫʱ���ɻ�����3.2��Ԫ��
��
|
���
|
���ԣ�yB=-
| 1 |
| 5 |
| 8 |
| 5 |
��2����Ͷ��B��Ʒx��Ԫ����Ͷ��A��Ʒ��10-x����Ԫ��
����y=-
| 1 |
| 5 |
| 8 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| 6 |
| 5 |
| 1 |
| 5 |
| 9 |
| 5 |
| 1 |
| 5 |
��y=-
| 1 |
| 5 |
���ԣ���Ͷ��B��Ʒ3��Ԫʱ���ܻ�õ��������
��ʱͶ��A��Ʒ7��Ԫ��B��Ʒ3��Ԫ��������������5.8��Ԫ��
��3��y=5ʱ��-
| 1 |
| 5 |
�����ã�x-3��2=4��
����x-3=2��x-3=-2��
���ԣ�x1=5��x2=1��
��a=-
| 1 |
| 5 |
��Ͷ��B��Ʒ1��5��Ԫʱ����õ�������5��Ԫ��
���������⿼����Ƕ��κ�����ʵ�������е�Ӧ�ã���Ҫ�����˴���ϵ��������������������κ����Ľ���ʽ�����κ�������ֵ���⣬�Լ����ö��κ��������ʽⲻ��ʽ���ۺ���ѶȲ���

��ϰ��ϵ�д�
�����Ŀ
������ʽA=
��B=
-
��������x�١�2������A��B�Ĺ�ϵ�ǣ�������
| 4 |
| x2-4 |
| 1 |
| x+2 |
| 1 |
| x-2 |
| A��A=B | B��AB=1 |
| C��A��B | D��A+B=0 |
 ��ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ���㣨-2��0���ͣ�x1��0��������1��x��2����y���������Ľ��㣨0��2�����·������н�����ȷ���ǣ�������
��ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ���㣨-2��0���ͣ�x1��0��������1��x��2����y���������Ľ��㣨0��2�����·������н�����ȷ���ǣ�������| A��abc��0 |
| B��9a+c��3b |
| C��a-b��0 |
| D��2a-b+1��0 |
����xΪδ֪���ķ��̣�3ax=10x-2a�Ľ���x=1����a��ֵΪ��������
A��
| ||
| B��1 | ||
C��
| ||
| D��2 |
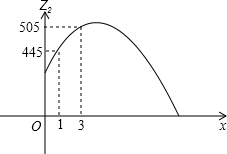 2012�����������������Ԥ����⣬����۸���1��3���µ����ѵ�����۵���͵㣻�������в˼ۣ�ȴ������һ��5Ԫһ�ѵ����ٲˡ�12Ԫ/ǧ�˵�Ģ����30Ԫ/ǧ�˵ĺڶ����Ǽ۳������˼۸�����ۡ�����ͨ���ձ�ʾ�Բ����أ�����3�£����ű����߲˵Ĵ������У������߲˼۸��ձ��½�������������ijһ����3�·�ÿ�ܵ�Ģ�����ۼ۸�仯���±���
2012�����������������Ԥ����⣬����۸���1��3���µ����ѵ�����۵���͵㣻�������в˼ۣ�ȴ������һ��5Ԫһ�ѵ����ٲˡ�12Ԫ/ǧ�˵�Ģ����30Ԫ/ǧ�˵ĺڶ����Ǽ۳������˼۸�����ۡ�����ͨ���ձ�ʾ�Բ����أ�����3�£����ű����߲˵Ĵ������У������߲˼۸��ձ��½�������������ijһ����3�·�ÿ�ܵ�Ģ�����ۼ۸�仯���±��� ������OABC�У�A���ڷ���������
������OABC�У�A���ڷ���������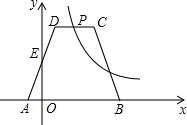 ��֪��ͼ����������ABCD�����Ϊ5��E��P�ֱ�ΪAD��CD���е㣬˫����
��֪��ͼ����������ABCD�����Ϊ5��E��P�ֱ�ΪAD��CD���е㣬˫���� ��������ί�ڶ�ȫ����ʡ��������2010������ΰ��ۺ����������У���������93.48�־�ȫ����һ����Ϊȫ���ȫ�����ȶ��ij���֮һ�� �������dz����ӽ�Ѳ��ƽ̨�Ľ��裬��ͳ�ƣ�ij��������ȥ��ǰ7�����ڣ���Ѳ��ƽ̨���������·�֮��Ĺ�ϵ���±���
��������ί�ڶ�ȫ����ʡ��������2010������ΰ��ۺ����������У���������93.48�־�ȫ����һ����Ϊȫ���ȫ�����ȶ��ij���֮һ�� �������dz����ӽ�Ѳ��ƽ̨�Ľ��裬��ͳ�ƣ�ij��������ȥ��ǰ7�����ڣ���Ѳ��ƽ̨���������·�֮��Ĺ�ϵ���±���