题目内容
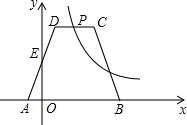 已知如图,等腰梯形ABCD的面积为5,E、P分别为AD、CD的中点,双曲线y=
已知如图,等腰梯形ABCD的面积为5,E、P分别为AD、CD的中点,双曲线y=| k |
| x |
考点:反比例函数综合题
专题:压轴题
分析:首先利用E、P分别为AD、CD的中点的即可得出△DNE≌△AOE,以及矩形NOMP的面积等于梯形DAMP的面积=
×5=
,即可得出双曲线y=
经过点P,则k=xy的值.
| 1 |
| 2 |
| 5 |
| 2 |
| k |
| x |
解答: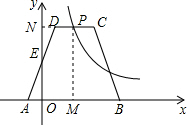 解:过点P作PM⊥AB于点M,延长CD到y轴于点N,
解:过点P作PM⊥AB于点M,延长CD到y轴于点N,
∵等腰梯形ABCD,E、P分别为AD、CD的中点,
∴NE=EO,梯形DAMP与梯形PMBC面积相等等于
等腰梯形ABCD的面积,
∵在△DNE和△AOE中,
,
∴△DNE≌△AOE(AAS),
∴矩形NOMP的面积等于梯形DAMP的面积=
×5=
,
∴双曲线y=
经过点P,则k=xy=
,
故答案为:
.
 解:过点P作PM⊥AB于点M,延长CD到y轴于点N,
解:过点P作PM⊥AB于点M,延长CD到y轴于点N,∵等腰梯形ABCD,E、P分别为AD、CD的中点,
∴NE=EO,梯形DAMP与梯形PMBC面积相等等于
| 1 |
| 2 |
∵在△DNE和△AOE中,
|
∴△DNE≌△AOE(AAS),
∴矩形NOMP的面积等于梯形DAMP的面积=
| 1 |
| 2 |
| 5 |
| 2 |
∴双曲线y=
| k |
| x |
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:此题主要考查了反比例函数的综合应用,根据已知得出矩形NOMP的面积等于梯形DAMP的面积是解题关键.

练习册系列答案
相关题目
圆锥主视图是正三角形,其母线与高的夹角是( )
| A、30° | B、45° |
| C、60° | D、90° |
一元二次方程x2-6x-15=0的两根x1、x2,则x12+x22的值是( )
| A、6 | B、36 | C、-6 | D、66 |
已知p,p+14,p+q都是质数,并且p有唯一的值和它对应,则q只能取( )
| A、40 | B、44 | C、74 | D、86 |
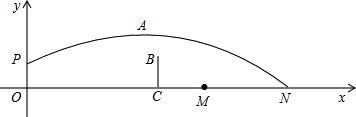
 小明欲将一块三角形的废料剪裁成一个圆形材料,为节约材料想剪载成最大的圆形材料,请帮忙确定该圆的圆心和半径.
小明欲将一块三角形的废料剪裁成一个圆形材料,为节约材料想剪载成最大的圆形材料,请帮忙确定该圆的圆心和半径.