题目内容
 2012年国家商务部发布了商务预报监测,猪肉价格在1~3月下跌后,已跌至肉价的最低点;而重庆市菜价,却在上演一轮5元一把的藤藤菜、12元/千克的蘑菇、30元/千克的黑豆的涨价潮,“菜价高于肉价”让普通百姓表示吃不起素.进入3月,随着本地蔬菜的大量上市,我市蔬菜价格普遍下降.以下是重庆某一超市3月份每周的蘑菇销售价格变化如下表:
2012年国家商务部发布了商务预报监测,猪肉价格在1~3月下跌后,已跌至肉价的最低点;而重庆市菜价,却在上演一轮5元一把的藤藤菜、12元/千克的蘑菇、30元/千克的黑豆的涨价潮,“菜价高于肉价”让普通百姓表示吃不起素.进入3月,随着本地蔬菜的大量上市,我市蔬菜价格普遍下降.以下是重庆某一超市3月份每周的蘑菇销售价格变化如下表:| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 12 | 6 | 4 | 3 |
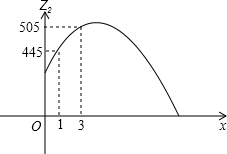
(1)请观察题中的表格及函数图象,用你所学过的一次函数、反比例函数或二次函数的有关知识,直接写出3月份每周的销售价格y(元/千克)与周数x(1≤x≤4,且x为整数)之间的函数关系式?并直接写出4月份每周的销售量z2(千克)与周数x(1≤x≤4,且x为整数)所满足的函数关系式?
(2)求出3月和4月分别在哪一周销售此种蘑菇的销售额最大?且最大销售额分别是多少?
(3)进入5月,重庆市由于受暴雨的影响,蔬菜运输道路堵塞,蔬菜及时供应困难,蘑菇的价格出现波动,5月的第1周蘑菇的销售价格比4月份上涨a%,销售量比4月的第4周增加0.5a%,5月份的第2周蘑菇的销售价格与5月的第1周持平,但销售量比第1周减少130千克,这样,要使5月份第2周的销售额达到4月份的最大销售额,求a的最小正整数值?(参考数据:
| 31 |
| 33 |
| 35 |
考点:二次函数的应用
专题:
分析:(1)设3月份每周的销售价格y(元/千克)与周数x(1≤x≤4,且x为整数)之间的函数关系式为y=
,根据函数图象直接利用待定系数法就可以求出4月份每周的销售量z2(千克)与周数x(1≤x≤4,且x为整数)之间的函数关系式;
(2)设销售额为w,根据销售额=销售单价×销售数量就可以分别把三月和四月各周的销售额表示出来,根据二次函数的顶点式就可以求出结论;
(3)先求出4月第四周的销售量为-5×16+50×4+400=520kg,就可以表示出5月第一周的销量为520(1+0.5a%)kg,第二周的销量为520(1+0.5a%)-130,再表示出5月第一周的价格3(1+a%)元,根据5月份第2周的销售额达到4月份的最大销售额为等量关系建立方程求出其解即可.
| k |
| x |
(2)设销售额为w,根据销售额=销售单价×销售数量就可以分别把三月和四月各周的销售额表示出来,根据二次函数的顶点式就可以求出结论;
(3)先求出4月第四周的销售量为-5×16+50×4+400=520kg,就可以表示出5月第一周的销量为520(1+0.5a%)kg,第二周的销量为520(1+0.5a%)-130,再表示出5月第一周的价格3(1+a%)元,根据5月份第2周的销售额达到4月份的最大销售额为等量关系建立方程求出其解即可.
解答:解:(1)设设3月份每周的销售价格y(元/千克)与周数x(1≤x≤4,且x为整数)之间的函数关系式为y=
,由题意,得
6=
,
∴k=12.
∴y=
(1≤x≤4,且x为整数),
∵z2=ax2+bx+400经过(1,455),(3,505)两点,
∴
,
解得:
,
∴z2=-5x2+50x+400;
(2)由题意,得
三月每周的销售额为:
w3月=
(-25x2+175x),
=-300x+2100,
∵k=-300<0,
∴w随x的增大而减小,
∴x=1时,w3月最大=1800元,
四月每周的销售额为:
w4月=3(-5x2+50x+400),
=-15(x-5)2+1575,
∵a=-15<0,
∴抛物线的开口向下,函数有最大值,在对称轴左侧w随x的增大而增大,
∵对称轴为x=5,1≤x≤4,且x为整数,
∴x=4时,w4月最大=1560元
∴三月的第一周销售额最大为1800元,4月的第四周销售额最大为1560元.
(3)由题意,得
4月第四周的销售量为:-5×16+50×4+400=520kg,
5月第一周的销量为:520(1+0.5a%)kg,
第二周的销量为:520(1+0.5a%)-130,
5月第一周的价格为:3(1+a%)元,
[520(1+0.5a%)-130]×3(1+a%)=1560,
化简为:2m2+5m-1=0,
m=
,
=
,
∵
≈5.745,
∴m1=0.18625,m2=-2.68625,
∴a%=0.18625或a%=-2.68625,
∴a=18.625或-268.625.
∵a为正整数,
∴a=19.
答:a的最小正整数值为19.
| k |
| x |
6=
| k |
| 2 |
∴k=12.
∴y=
| 12 |
| x |
∵z2=ax2+bx+400经过(1,455),(3,505)两点,
∴
|
解得:
|
∴z2=-5x2+50x+400;
(2)由题意,得
三月每周的销售额为:
w3月=
| 12 |
| x |
=-300x+2100,
∵k=-300<0,
∴w随x的增大而减小,
∴x=1时,w3月最大=1800元,
四月每周的销售额为:
w4月=3(-5x2+50x+400),
=-15(x-5)2+1575,
∵a=-15<0,
∴抛物线的开口向下,函数有最大值,在对称轴左侧w随x的增大而增大,
∵对称轴为x=5,1≤x≤4,且x为整数,
∴x=4时,w4月最大=1560元
∴三月的第一周销售额最大为1800元,4月的第四周销售额最大为1560元.
(3)由题意,得
4月第四周的销售量为:-5×16+50×4+400=520kg,
5月第一周的销量为:520(1+0.5a%)kg,
第二周的销量为:520(1+0.5a%)-130,
5月第一周的价格为:3(1+a%)元,
[520(1+0.5a%)-130]×3(1+a%)=1560,
化简为:2m2+5m-1=0,
m=
-5±
| ||
| 4 |
=
-5±
| ||
| 4 |
∵
| 33 |
∴m1=0.18625,m2=-2.68625,
∴a%=0.18625或a%=-2.68625,
∴a=18.625或-268.625.
∵a为正整数,
∴a=19.
答:a的最小正整数值为19.
点评:本题考查了运用待定系数法求反比例函数和二次函数的解析式的运用,二次函数的顶点式的运用和一次函数的性质的运用,列一元二次方程解实际问题的运用及一元二次方程的额解法的运用,解答第三问是难点,根据题意的数量关系建立方程是解答的关键.本题也是今年来中考的常考题型,属于高难度题,计算量较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆锥主视图是正三角形,其母线与高的夹角是( )
| A、30° | B、45° |
| C、60° | D、90° |
一元二次方程x2-6x-15=0的两根x1、x2,则x12+x22的值是( )
| A、6 | B、36 | C、-6 | D、66 |
据官方统计,截止2012年11月15日镇海财政收入突破七十亿,公共财政收入达7031000000元,则此公共财政收入用科学记数法可记为( )
| A、70.31×108 |
| B、7.031×109 |
| C、7031106 |
| D、7.031×103 |
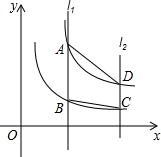 如图,平行于y轴的直线l1分别与双曲线
如图,平行于y轴的直线l1分别与双曲线