题目内容
1.在平面直角坐标系中,△ABC的顶点坐标分别为A(2,1),B(6,1),C(6,3),将△ABC平移后得到的顶点坐标可能是A′(2,3),B′(6,3),C′(6,6)吗?请说明理由.分析 利用平移中点的变化规律即可说明理由.
解答 解:将△ABC平移后得到的顶点坐标不可能是A′(2,3),B′(6,3),C′(6,6).理由如下:
∵△ABC的顶点坐标分别为A(2,1),B(6,1),C(6,3),
∴将△ABC向上平移2个单位后得到的对应顶点坐标是(2,3),(6,3),C′(6,5),
∵C′(6,6),
∴不可能.
点评 本题考查了坐标系中点、图形的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.

练习册系列答案
相关题目
9.计算(-$\frac{1}{2}$)2016+(-$\frac{1}{2}$)2017得( )
| A. | -$\frac{1}{{2}^{2017}}$ | B. | -$\frac{1}{{2}^{2016}}$ | C. | ($\frac{1}{2}$)2017 | D. | ($\frac{1}{2}$)2016 |
13.下列计算中,正确的是( )
| A. | 2×2-2=$\frac{1}{2}$ | B. | (-9)0=-1 | C. | 3a-2=$\frac{1}{3{a}^{2}}$(a≠0) | D. | a5×a-3=a5÷a3 |
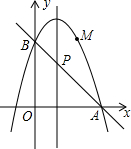 已知二次函数y=-x2+2x+m
已知二次函数y=-x2+2x+m 如图,已知直线AB∥CD,BC∥DE,若∠B=60°,则∠D=120°.
如图,已知直线AB∥CD,BC∥DE,若∠B=60°,则∠D=120°.