题目内容
15.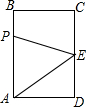 如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.
如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.
分析 分P在AB上、P在BC上、P在CE上三种情况,根据三角形的面积公式计算即可.
解答 解:当P在AB上时,
∵△APE的面积等于5,
∴$\frac{1}{2}$x•3=5,
x=$\frac{10}{3}$;
当P在BC上时,
∵△APE的面积等于5,
∴S矩形ABCD-S△CPE-S△ADE-S△ABP=5,
∴3×4-$\frac{1}{2}$(3+4-x)×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×4×(x-4)=5,
x=5;
③当P在CE上时,
$\frac{1}{2}$(4+3+2-x)×3=5,
x=$\frac{17}{3}$(不合题意),
故答案为:$\frac{10}{3}$或5.
点评 本题考查的是三角形的面积计算,灵活运用分情况讨论思想是解题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
10.下列各式中,计算错误的是( )
| A. | [(a+b)2]5=(a+b)10 | B. | [(a+b)2]n=(a+b)n+2 | C. | [(a+b)x]5=(a+b)5x | D. | [(a+b)m]n=(a+b)mn |
6.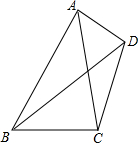 如图,四边形ABCD中,AC=6,BD=8,AC与BD所夹锐角为60°,则四边形ABCD的面积为( )
如图,四边形ABCD中,AC=6,BD=8,AC与BD所夹锐角为60°,则四边形ABCD的面积为( )
 如图,四边形ABCD中,AC=6,BD=8,AC与BD所夹锐角为60°,则四边形ABCD的面积为( )
如图,四边形ABCD中,AC=6,BD=8,AC与BD所夹锐角为60°,则四边形ABCD的面积为( )| A. | 12 | B. | 12$\sqrt{3}$ | C. | 24 | D. | 24$\sqrt{3}$ |
3.若a+b=2,则代数式a2-b2+4b的值是( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
7.下列根式中:$\sqrt{2a}$,$\sqrt{1+a}$,$\sqrt{{a}^{2}+{b}^{2}}$,$\sqrt{{n}^{2}+2n+1}$,$\sqrt{10}$,$\sqrt{12}$,是最简二次根式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
5.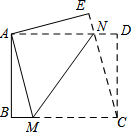 如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )
如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )
 如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )
如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )| A. | 5 | B. | 4 | C. | $\sqrt{20}$ | D. | $\sqrt{24}$ |
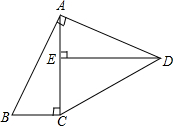 如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.
如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD. 如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)
如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)