题目内容
5.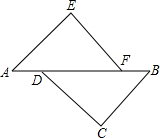 如图,A、D、F、B在同一直线上,AD=BF,AE=BC,∠A=∠B,求证:EF∥CD.
如图,A、D、F、B在同一直线上,AD=BF,AE=BC,∠A=∠B,求证:EF∥CD.
分析 根据已知条件得出△AEF≌△BCD,即可得出∠AFE=∠BDC,再根据内错角相等两直线平行,即可证明EF∥CD.
解答 证明:∵AD=BF,
∴AD+EF=BF+EF,
∴AF=BD,
在△ACB和△DEF中,
$\left\{\begin{array}{l}{AF=BD}\\{∠A=∠B}\\{AE=BC}\end{array}\right.$,
∴△ACB≌△DEF(SAS),
∴∠AFE=∠BDC,
∴EF∥CD.
点评 本题考查了两直线平行的判定方法,内错角相等,两直线平行,解决本题的关键是证明△ACB≌△DEF,得到∠AFE=∠BDC,即可解答.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
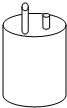 如图:两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是该铁棒的$\frac{1}{3}$,另一根露出水面的长度是该铁棒的$\frac{1}{4}$,两根铁棒长度之和为51厘米,求此木桶中水的深度是多少厘米?
如图:两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是该铁棒的$\frac{1}{3}$,另一根露出水面的长度是该铁棒的$\frac{1}{4}$,两根铁棒长度之和为51厘米,求此木桶中水的深度是多少厘米?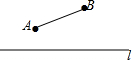 公路l同侧的A、B两村,共同出资在公路边修建一个客车停靠站C,并使停靠站到A、B两村的距离相等,你如何确定停靠站C的位置.利用尺规作图作出点C,写出作法,并保留作图痕迹.
公路l同侧的A、B两村,共同出资在公路边修建一个客车停靠站C,并使停靠站到A、B两村的距离相等,你如何确定停靠站C的位置.利用尺规作图作出点C,写出作法,并保留作图痕迹. 如图,在△ABC中,∠B=30°,∠C=66°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.
如图,在△ABC中,∠B=30°,∠C=66°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.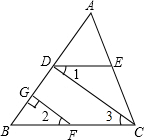 如图,CD⊥AB,GF⊥AB,∠B=∠ADE,试说明:∠CDE=∠BFG.
如图,CD⊥AB,GF⊥AB,∠B=∠ADE,试说明:∠CDE=∠BFG.