题目内容
13.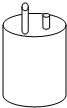 如图:两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是该铁棒的$\frac{1}{3}$,另一根露出水面的长度是该铁棒的$\frac{1}{4}$,两根铁棒长度之和为51厘米,求此木桶中水的深度是多少厘米?
如图:两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是该铁棒的$\frac{1}{3}$,另一根露出水面的长度是该铁棒的$\frac{1}{4}$,两根铁棒长度之和为51厘米,求此木桶中水的深度是多少厘米?
分析 设较长铁棒的长度为xcm,较短铁棒的长度为ycm.因为两根铁棒之和为51cm,故可的方程:x+y=51,又知两棒未露出水面的长度相等,又可得方程$\frac{2}{3}$x=$\frac{3}{4}$y,把两个方程联立,组成方程组,解方程组可得较长的铁棒的长度,用较长的铁棒的长度×$\frac{2}{3}$可以求出木桶中水的深度.
解答 解:设较长铁棒的长度为xcm,较短铁棒的长度为ycm,由题意得:
$\left\{\begin{array}{l}{x+y=51}\\{\frac{2}{3}x=\frac{3}{4}y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=27}\\{y=24}\end{array}\right.$,
因此木桶中水的深度为27×$\frac{2}{3}$=18(cm),
答:此木桶中水的深度是18厘米.
点评 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,找出合适的等量关系,列方程组求解.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
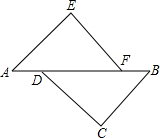 如图,A、D、F、B在同一直线上,AD=BF,AE=BC,∠A=∠B,求证:EF∥CD.
如图,A、D、F、B在同一直线上,AD=BF,AE=BC,∠A=∠B,求证:EF∥CD.