题目内容
11. 小明把一根长160cm的竹条做成一个等腰三角形的风筝的边框(如图),已知该三角形的底边上的高AD=40cm,请问AB、AC、BC的长分别是多少?
小明把一根长160cm的竹条做成一个等腰三角形的风筝的边框(如图),已知该三角形的底边上的高AD=40cm,请问AB、AC、BC的长分别是多少?
分析 设出腰的长,则底边的长可表示出来,又已知等腰三角形的高,在Rt△ABD中运用勾股定理可解得腰长.
解答 解:设腰长AB=AC=xcm,则BC=160-2x,BD=$\frac{1}{2}$BC=80-x,
在Rt△ABD中,AB2=BD2+AD2,
即x2=(80-x)2+402,
解之得:x=50,
∴AB=AC=50cm,BC=160-2×50=60cm.
点评 本题考查了等腰三角形的性质,解答本题的关键是掌握等腰三角形三线合一的性质以及勾股定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图,在△ABC中,AB=AC,AD是高,能直接判断△ABD≌△ACD的依据是( )
如图,在△ABC中,AB=AC,AD是高,能直接判断△ABD≌△ACD的依据是( )
 如图,在△ABC中,AB=AC,AD是高,能直接判断△ABD≌△ACD的依据是( )
如图,在△ABC中,AB=AC,AD是高,能直接判断△ABD≌△ACD的依据是( )| A. | SSS | B. | SAS | C. | HL | D. | ASA |

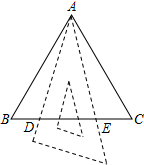 如图,△ABC是边长为a的等边三角形,将三角板的30°角的顶点与A重合,三角板30°角的两边与BC交于D、E两点,则DE长度的取值范围是(2$\sqrt{3}$-3)a≤DE≤$\frac{1}{2}$a..
如图,△ABC是边长为a的等边三角形,将三角板的30°角的顶点与A重合,三角板30°角的两边与BC交于D、E两点,则DE长度的取值范围是(2$\sqrt{3}$-3)a≤DE≤$\frac{1}{2}$a..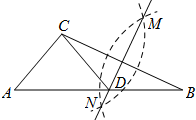 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为105°.
如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为105°. 一个等腰三角形工件,尺寸标注如图,则△ABC的面积为512$\sqrt{21}$mm2.
一个等腰三角形工件,尺寸标注如图,则△ABC的面积为512$\sqrt{21}$mm2.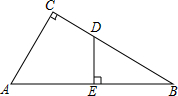 如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.
如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.