题目内容
3.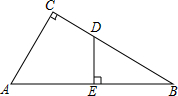 如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.
如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.
分析 根据相似三角形的判定与性质,可得答案.
解答 解:∵DE⊥AB,
∴∠BED=90°,
又∠C=90°,
∴∠BED=∠C.
又∠B=∠B,
∴△BED∽△BCA,
∴$\frac{BD}{AB}$=$\frac{DE}{AC}$,
∴DE=$\frac{BD•AC}{AB}$=$\frac{8×7}{14}$=4
点评 本题考查了相似三角形的判定与性质,利用相似三角形的性质得出$\frac{BD}{AB}$=$\frac{DE}{AC}$是解题关键.

练习册系列答案
相关题目
18.将下列四种长度的三根木棒首尾顺次连接,能组成三角形的是( )
| A. | 2,5,8 | B. | 3,4,5 | C. | 2,2,4 | D. | 1,2,3 |
8.已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为( )
| A. | 28° | B. | 112° | C. | 28°或112° | D. | 68° |
12.( )的倒数是-$\frac{1}{2}$.
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图: 小明把一根长160cm的竹条做成一个等腰三角形的风筝的边框(如图),已知该三角形的底边上的高AD=40cm,请问AB、AC、BC的长分别是多少?
小明把一根长160cm的竹条做成一个等腰三角形的风筝的边框(如图),已知该三角形的底边上的高AD=40cm,请问AB、AC、BC的长分别是多少?