Question

16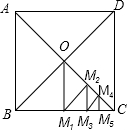．如图，正方形ABCD的边长为4，它的两条对角线交于点O，过点0作边BC的垂线，垂足为M₁，△OBM₁的面积为S₁，过点M₁作OC的垂线，垂足为M₂，△△OM₁M₂的面积为S₂，过点M₂作BC的垂线，垂足为M₃，△M₁M₂M₃的面积为S₃，…△M_n-2M_n-1M_n的面积为S_n，则S₁+S₂+S₃+…+S_n=（　　）

• A． 4
• B． 4-（$\frac{1}{2}$）^n-1
• C． 4-（$\frac{1}{2}$）^n-2
• D． 4-（$\frac{1}{2}$）^n-3

Answer 1

分析 由正方形的性质得出S₁、S₂、S₃、S₄、S₅，…，得出规律，再求出它们的和即可．

解答 解：∵四边形ACD是正方形，
∴OB=OC，AC⊥BD，S₁=$\frac{1}{4}$×4×4×$\frac{1}{2}$=2，S₂=$\frac{1}{2}$×2=1，
S₃=$\frac{1}{2}$×1=$\frac{1}{2}$，S₄=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$=$\frac{1}{{2}^{2}}$，S₅=$\frac{1}{2}$×$\frac{1}{4}$=$\frac{1}{8}$=$\frac{1}{{2}^{3}}$，…，S_n=$\frac{1}{{2}^{n-2}}$，
∴S₁+S₂+S₃+…+S_n=2+1+$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n-2}}$，
=4-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{8}$+…+$\frac{1}{{2}^{n-3}}$-$\frac{1}{{2}^{n-2}}$
=4-$\frac{1}{{2}^{n-2}}$
=4-（$\frac{1}{2}$）^n-2；
故选：C．

点评 本题考查了正方形的性质、三角形面积的计算；通过计算三角形的面积得出规律是解决问题的关键．