题目内容
1.(1)解方程:$\frac{3}{x}$=$\frac{2}{x+1}$;(2)解不等式组:$\left\{\begin{array}{l}{x-3≤0}\\{3(x-1)-2(2x-1)<1}\end{array}\right.$,并求该不等式组的整数解.
分析 (1)首先同时乘以x(x+1)去分母可得3(x+1)=2x,再解方程即可;
(2)分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可.
解答 解:(1)去分母得:3(x+1)=2x,
3x+3=2x,
x=-3,
检验:把x=-3代入x(x+1)≠0,因此x=-3是原分式方程的解;
(2)由①得:x≤3,
由②得:x>-2,
则不等式组的解集为:-2<x≤-3,
因此不等式组的整数解为-1,0,1,2,3.
点评 此题主要考查了分式方程和一元一次不等式组的解法,关键是掌握不等式组解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.注意分式方程不要忘记检验.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.目前,我国大约有1.3亿高血压病患者,预防高血压不容忽视.“千帕kpa”和“毫米汞柱mmHg”都是表示血压的单位.请你根据表格提供的信息,判断下列各组换算正确的是( )
| 千帕kpa | … | 10 | 12 | 14 | … |
| 毫米汞柱mmHg | … | 75 | 90 | 105 | … |
| A. | 6kpa=50mmHg | B. | 16kpa=110mmHg | C. | 20kpa=150mmHg | D. | 22kpa=160mmHg |
9.“每天锻炼一小时,健康生活一辈子”.新泰市自开展“阳光体育运动”以来,学校师生的锻炼意识都增强了,某校有学生3000人,为了解学生每天的锻炼时间,学校体育组随机调查了部分学生,统计结果如表所示.
该校每天锻炼时间达到1小时及以上的约有300人.
| 时间段 | 29分钟及以下 | 30-39分钟 | 40-49分钟 | 50-59分钟 | 1小时及以上 |
| 频数/人 | 108 | 20 | |||
| 频率 | 0.54 | 0.12 | 0.09 |
16.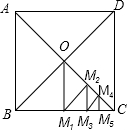 如图,正方形ABCD的边长为4,它的两条对角线交于点O,过点0作边BC的垂线,垂足为M1,△OBM1的面积为S1,过点M1作OC的垂线,垂足为M2,△△OM1M2的面积为S2,过点M2作BC的垂线,垂足为M3,△M1M2M3的面积为S3,…△Mn-2Mn-1Mn的面积为Sn,则S1+S2+S3+…+Sn=( )
如图,正方形ABCD的边长为4,它的两条对角线交于点O,过点0作边BC的垂线,垂足为M1,△OBM1的面积为S1,过点M1作OC的垂线,垂足为M2,△△OM1M2的面积为S2,过点M2作BC的垂线,垂足为M3,△M1M2M3的面积为S3,…△Mn-2Mn-1Mn的面积为Sn,则S1+S2+S3+…+Sn=( )
 如图,正方形ABCD的边长为4,它的两条对角线交于点O,过点0作边BC的垂线,垂足为M1,△OBM1的面积为S1,过点M1作OC的垂线,垂足为M2,△△OM1M2的面积为S2,过点M2作BC的垂线,垂足为M3,△M1M2M3的面积为S3,…△Mn-2Mn-1Mn的面积为Sn,则S1+S2+S3+…+Sn=( )
如图,正方形ABCD的边长为4,它的两条对角线交于点O,过点0作边BC的垂线,垂足为M1,△OBM1的面积为S1,过点M1作OC的垂线,垂足为M2,△△OM1M2的面积为S2,过点M2作BC的垂线,垂足为M3,△M1M2M3的面积为S3,…△Mn-2Mn-1Mn的面积为Sn,则S1+S2+S3+…+Sn=( )| A. | 4 | B. | 4-($\frac{1}{2}$)n-1 | C. | 4-($\frac{1}{2}$)n-2 | D. | 4-($\frac{1}{2}$)n-3 |
6. 如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )
如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )
 如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )
如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.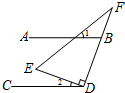 如图,直线AB∥CD,Rt△DEF如图放置,∠EDF=90°,若∠1+∠F=70°,则∠2的度数为( )
如图,直线AB∥CD,Rt△DEF如图放置,∠EDF=90°,若∠1+∠F=70°,则∠2的度数为( )
 如图,直线AB∥CD,Rt△DEF如图放置,∠EDF=90°,若∠1+∠F=70°,则∠2的度数为( )
如图,直线AB∥CD,Rt△DEF如图放置,∠EDF=90°,若∠1+∠F=70°,则∠2的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
10.在下面的四个几何体中,它们各自的左视图与主视图不相同的是( )
| A. | 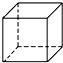 正方体 | B. | 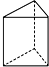 三棱柱 | C. |  圆柱 | D. |  圆锥 |
 如图所示是函数y=-$\frac{3}{4}$x+3的图象,那么方程-$\frac{3}{4}$x+3=0的解是x=4,不等式-$\frac{3}{4}$x+3<0的解集是x>4,当y>3时,x的取值范围是x<0.
如图所示是函数y=-$\frac{3}{4}$x+3的图象,那么方程-$\frac{3}{4}$x+3=0的解是x=4,不等式-$\frac{3}{4}$x+3<0的解集是x>4,当y>3时,x的取值范围是x<0.