题目内容
5.【阅读学习】刘老师提出这样一个问题:已知α为锐角,且tanα=$\frac{1}{3}$,求sin2α的值.
小娟是这样解决的:
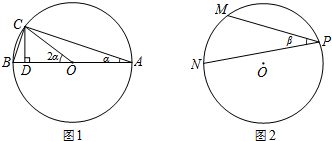
如图1,在⊙O中,AB是直径,点C在⊙O上,∠BAC=α,所以∠ACB=90°,tanα=$\frac{BC}{AC}$=$\frac{1}{3}$.
易得∠BOC=2α.设BC=x,则AC=3x,则AB=$\sqrt{10}$x.作CD⊥AB于D,求出CD=$\frac{3\sqrt{10}}{10}$x(用含x的式子表示),可求得sin2α=$\frac{CD}{OC}$=$\frac{3}{5}$.
【问题解决】
已知,如图2,点M、N、P为圆O上的三点,且∠P=β,tanβ=$\frac{1}{2}$,求sin2β的值.
分析 【阅读学习】根据三角形的面积公式可得S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,求出CD=$\frac{AC•BC}{AB}$=$\frac{3\sqrt{10}}{10}$x.由AB=$\sqrt{10}$x,得出OC=$\frac{1}{2}$AB=$\frac{\sqrt{10}}{2}$x,从而计算得出sin2α=$\frac{CD}{OC}$=$\frac{3}{5}$;
【问题解决】连接NO,并延长交⊙O于Q,连接MQ,MO,作MH⊥NO于H.首先根据圆周角定理得出∠NMQ=90°.利用圆周角定理、等腰三角形的性质及三角形外角的性质得出∠MON=2∠Q=2β.再由tanβ=$\frac{1}{2}$,可设MN=k,则MQ=2k,利用勾股定理求出NQ=$\sqrt{M{N^2}+M{Q^2}}=\sqrt{5}k$,则OM=$\frac{1}{2}$NQ=$\frac{{\sqrt{5}}}{2}k$.根据三角形的面积公式可求得MH=$\frac{{2\sqrt{5}}}{5}k$,然后在Rt△MHO中利用正弦函数的定义即可求出sin2β的值.
解答 解:【阅读学习】
∵S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
∴CD=$\frac{AC•BC}{AB}$=$\frac{3x•x}{\sqrt{10}x}$=$\frac{3\sqrt{10}}{10}$x.
∵AB=$\sqrt{10}$x,
∴OC=$\frac{1}{2}$AB=$\frac{\sqrt{10}}{2}$x,
∴sin2α=$\frac{CD}{OC}$=$\frac{\frac{3\sqrt{10}}{10}x}{\frac{\sqrt{10}}{2}x}$=$\frac{3}{5}$.
故答案为$\frac{3\sqrt{10}}{10}$x,$\frac{3}{5}$;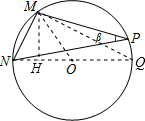 【问题解决】
【问题解决】
如图,连接NO,并延长交⊙O于Q,连接MQ,MO,作MH⊥NO于H.
在⊙O中,∠NMQ=90°.
∵∠Q=∠P=β,OM=ON,
∴∠MON=2∠Q=2β.
∵tanβ=$\frac{1}{2}$,
∴设MN=k,则MQ=2k,
∴NQ=$\sqrt{M{N^2}+M{Q^2}}=\sqrt{5}k$.
∴OM=$\frac{1}{2}$NQ=$\frac{{\sqrt{5}}}{2}k$.
∵${S_{△NMQ}}=\frac{1}{2}MN•MQ=\frac{1}{2}NQ•MH$,
∴$k•2k=\sqrt{5}k•MH$.
∴MH=$\frac{{2\sqrt{5}}}{5}k$.
在Rt△MHO中,sin2β=sin∠MON=$\frac{MH}{OM}=\frac{{\frac{{2\sqrt{5}}}{5}k}}{{\frac{{\sqrt{5}k}}{2}}}=\frac{4}{5}$.
点评 本题考查了解直角三角形,三角形的面积,锐角三角函数的定义,勾股定理,圆周角定理,等腰三角形的性质,三角形外角的性质等知识,有一定难度.准确作出辅助线构造直角三角形是解题的关键.

| 第1组 | 35 | 36 | 38 | 40 | 42 | 42 | 75 |
| 第2组 | 35 | 36 | 38 | 40 | 42 | 42 | 45 |
(2)比较两组数据的平均数、众数、中位数,并谈谈对它们的认识.
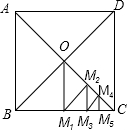 如图,正方形ABCD的边长为4,它的两条对角线交于点O,过点0作边BC的垂线,垂足为M1,△OBM1的面积为S1,过点M1作OC的垂线,垂足为M2,△△OM1M2的面积为S2,过点M2作BC的垂线,垂足为M3,△M1M2M3的面积为S3,…△Mn-2Mn-1Mn的面积为Sn,则S1+S2+S3+…+Sn=( )
如图,正方形ABCD的边长为4,它的两条对角线交于点O,过点0作边BC的垂线,垂足为M1,△OBM1的面积为S1,过点M1作OC的垂线,垂足为M2,△△OM1M2的面积为S2,过点M2作BC的垂线,垂足为M3,△M1M2M3的面积为S3,…△Mn-2Mn-1Mn的面积为Sn,则S1+S2+S3+…+Sn=( )| A. | 4 | B. | 4-($\frac{1}{2}$)n-1 | C. | 4-($\frac{1}{2}$)n-2 | D. | 4-($\frac{1}{2}$)n-3 |
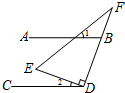 如图,直线AB∥CD,Rt△DEF如图放置,∠EDF=90°,若∠1+∠F=70°,则∠2的度数为( )
如图,直线AB∥CD,Rt△DEF如图放置,∠EDF=90°,若∠1+∠F=70°,则∠2的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
| A. |  正方体 | B. |  三棱柱 | C. |  圆柱 | D. |  圆锥 |
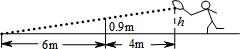 在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h=1.5m.
在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h=1.5m.