题目内容
2．若2011a+2012b=0，则ab是（ ）| A． | 正数 | B． | 非正数 | C． | 负数 | D． | 非负数 |
分析 当a，b为0时，可得ab是0；当a，b不为0时，将2011a+2012b=0变形为2011a=-2012b，可得$\frac{a}{b}$=-$\frac{2012}{2011}$＜0，根据有理数的除法法则可得a，b异号，再根据有理数的乘法法则即可求解．
解答 解：当a，b为0时，ab是0；
当a，b不为0时，
2011a+2012b=0，
2011a=-2012b，
$\frac{a}{b}$=-$\frac{2012}{2011}$＜0，
则a，b异号，
则ab是负数．
综上所述，ab是非正数．
故选：B．
点评 此题考查了有理数的乘法，关键是熟练掌握计算法则正确进行计算，注意分两种情况讨论．
练习册系列答案
阅读快车系列答案
相关题目
10．A、B两地分别有水泥20吨和30吨，C、D两地分别需要水泥15吨和35吨，现将A、B两地的水泥全部运到C、D两地，且恰好满足C、D两地的需要．若从A地运到C地的水泥为x吨，且将水泥从A、B两地运到C、D两地的运价如下表：
解答下列问题：
（1）用含x的式子表示从A地运到D地的水泥为（20-x）吨，从A地将水泥运到D地的运输费用为12（20-x）元．（答案直接填在题中横线上）
（2）用含x的代数式表示将水泥从A、B两地运到C、D两地的总运输费，并化简该式子．
（3）当x=10时，总运输费用为多少元？
（4）请写出总运输费用最少的运输方案．
| 到C地 | 到D地 | |
| A地 | 每吨15元 | 每吨12元 |
| B地 | 每吨10元 | 每吨9元 |
（1）用含x的式子表示从A地运到D地的水泥为（20-x）吨，从A地将水泥运到D地的运输费用为12（20-x）元．（答案直接填在题中横线上）
（2）用含x的代数式表示将水泥从A、B两地运到C、D两地的总运输费，并化简该式子．
（3）当x=10时，总运输费用为多少元？
（4）请写出总运输费用最少的运输方案．
17．下列说法正确的是（ ）
| A． | 若|a|=-a，则a＜0 | B． | 若a＜0，ab＜0，则b＞0 | ||
| C． | 若ab＞0，则a＞0，b＞0 | D． | 若a=b，m是有理数，则$\frac{a}{m}$=$\frac{b}{m}$ |
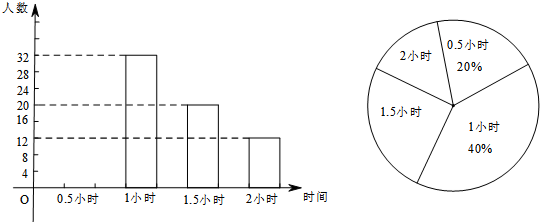
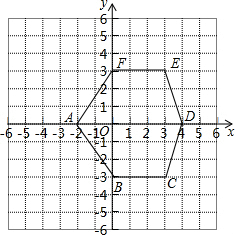如图是一个平面直角坐标系，按要求完成下列各小题．