题目内容
17.下列说法正确的是( )| A. | 若|a|=-a,则a<0 | B. | 若a<0,ab<0,则b>0 | ||
| C. | 若ab>0,则a>0,b>0 | D. | 若a=b,m是有理数,则$\frac{a}{m}$=$\frac{b}{m}$ |
分析 A、根据绝对的性质可得|a|=-a,则a≤0,
B、根据有理数的乘法法则:两数相乘,同号得正,异号得负可得:若ab<0,则a、b异号,由a<0,则b>0;
C、根据有理数的乘法法则:两数相乘,同号得正,异号得负可得:若ab>0,则a、b同号,同为正数或同为负数;
D、若a=b,根据等式的性质,等式的两边同时除以一个不为0的有理数,所得结果仍是等式.
解答 解:A、若|a|=-a,则a≤0,所以此选项说法错误;
B、若a<0,ab<0,则b>0,所以此选项说法正确;
C、若ab>0,则a>0,b>0或a<0,b<0;所以此选项说法错误,
D、若a=b,m≠0时,且m是有理数,则$\frac{a}{m}$=$\frac{b}{m}$,所以此选项说法错误;
故选B.
点评 此题主要考查了等式的性质,以及有理数的乘法和绝对值,关键是熟练掌握各计算法则.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
5.现对某商品进行打七折促销,为了使销售总金额不变,销售量要比按原价销售时增加几分之几?( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{9}$ |
2.若2011a+2012b=0,则ab是( )
| A. | 正数 | B. | 非正数 | C. | 负数 | D. | 非负数 |
7.某工厂计划招聘A、B两个工种的工人共120人,A、B两个工种的工人月工资分别为1600元和2000元.
(1)若某工厂每月支付的工人工资为220000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人,根据题设完成下列表格,并列方程求解
(2)设工厂每月支付的工人工资y元,试写出y与x之间的函数表达式,若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?
(1)若某工厂每月支付的工人工资为220000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人,根据题设完成下列表格,并列方程求解
(2)设工厂每月支付的工人工资y元,试写出y与x之间的函数表达式,若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?
| 工种 | 工人每月工资(元) | 招聘人数 | 工厂应付工人的约工资(元) |
| A | 1600 | x | 1600x |
| B | 2000 | 120-x | 2000(120-x) |
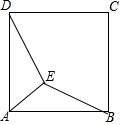 如图,点E是正方形ABCD内一点,DE=2,AE=1,EB=$\sqrt{2}$
如图,点E是正方形ABCD内一点,DE=2,AE=1,EB=$\sqrt{2}$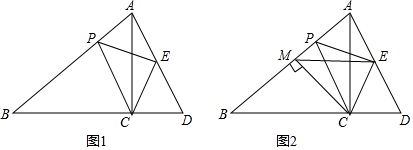
 如图,直线y=mx与y=-$\frac{1}{x}$和y=$\frac{k}{x}$分别交于A,B两点,且OB=2OA,则k=-4.
如图,直线y=mx与y=-$\frac{1}{x}$和y=$\frac{k}{x}$分别交于A,B两点,且OB=2OA,则k=-4.