题目内容
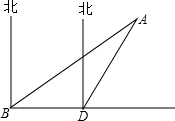天然气管道铺设工程从B向正东方向进行，如图所示，从B处测得A点位于B点北偏东60°，从B向东前进400m到达D点，在D点测得A点位于北偏东45°方向，以A点为中心，半径为500m的圆形区域为居民住宅区，请计算后回答：天然气管道铺设工程是否会穿过居民住宅区？（| 3 |
考点：解直角三角形的应用-方向角问题
专题：
分析：过点A作AC⊥BD于点C，先求出∠CBA=30°，AC=CD，设AC=CD=x，则BC=400+x，再根据tan30°=
=
，求出x的值，最后与500比较即可．
| AC |
| BC |
| x |
| 400+x |
解答：
解：过点A作AC⊥BD于点C，
∵从B处测得A点位于B点北偏东60°，
∴∠CBA=30°，
∵在D点测得A点位于北偏东45°方向，
∴AC=CD，
设AC=CD=x，
∵BD=400，
∴BC=400+x，
∴tan30°=
=
，
∴
=
，
解得：x=200
+200≈546.4＞500，
∴天然气管道铺设工程不会穿过居民住宅区．
解：过点A作AC⊥BD于点C，∵从B处测得A点位于B点北偏东60°，
∴∠CBA=30°，
∵在D点测得A点位于北偏东45°方向，
∴AC=CD，
设AC=CD=x，
∵BD=400，
∴BC=400+x，
∴tan30°=
| AC |
| BC |
| x |
| 400+x |
∴
| ||
| 3 |
| x |
| 400+x |
解得：x=200
| 3 |
∴天然气管道铺设工程不会穿过居民住宅区．
点评：此题主要考查了方向角问题，求三角形的边或高的问题一般可以转化为解直角三角形的问题，关键是作出高线，构造直角三角形．
练习册系列答案
阳光课堂课时作业系列答案
相关题目