题目内容
已知点A(2,-3)在抛物线y=x2-2x+m上,求经过点A且与抛物线只有一个公共点的直线解析式.
考点:二次函数的性质
专题:
分析:首先将点A的坐标代入都抛物线的解析式求得m的值,然后利用直线与抛物线只有一个交点求得直线的解析式即可;
解答:解:∵点A(2,-3)在抛物线y=x2-2x+m上,
∴-3=22-2×2+m,
解得:m=-3
设经过点A且与抛物线只有一个公共点的直线解析式为y=kx+b
∴2k+b=-3
∴b=-3-2k,
∴经过点A且与抛物线只有一个公共点的直线解析式为y=kx-3-2k,
∵与抛物线只有一个公共点
∴kx-3-2k=x2-2x-3只有一个实数根,
∴k=2,
b=-3-2k=-7,
∴直线的解析式为y=2k-7.
∴-3=22-2×2+m,
解得:m=-3
设经过点A且与抛物线只有一个公共点的直线解析式为y=kx+b
∴2k+b=-3
∴b=-3-2k,
∴经过点A且与抛物线只有一个公共点的直线解析式为y=kx-3-2k,
∵与抛物线只有一个公共点
∴kx-3-2k=x2-2x-3只有一个实数根,
∴k=2,
b=-3-2k=-7,
∴直线的解析式为y=2k-7.
点评:本题考查了二次函数性质,正确的设出解析式并用一个系数表示出另一个系数是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
使式子
有意义的x的取值范围是( )
| ||
| x-2 |
| A、x≠2 |
| B、x>-3且x≠2 |
| C、x≥3且x≠2 |
| D、x≥-3且x≠2 |
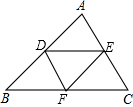 如图,在△ABC中,D,E,F分别在△ABC的三边上,且DE∥BC,DF∥AC,EF∥AB,则图中平行四边形有( )
如图,在△ABC中,D,E,F分别在△ABC的三边上,且DE∥BC,DF∥AC,EF∥AB,则图中平行四边形有( )| A、4个 | B、3个 | C、2个 | D、1个 |
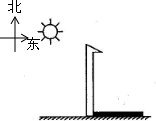 如图是王老师出示的他昨天画的一幅写生画,四个同学猜测他画这幅画的时间.请根据王老师给出的方向坐标,判断说的时间比较接近的是( )
如图是王老师出示的他昨天画的一幅写生画,四个同学猜测他画这幅画的时间.请根据王老师给出的方向坐标,判断说的时间比较接近的是( )| A、小丽说:“早上8时” |
| B、小强说:“中午12时” |
| C、小刚说:“下午5时” |
| D、小明说:“哪个时间段都行” |
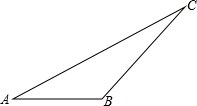 如图所示,已知在△ABC中,∠A=30°,∠B=135°,AC=8.求△ABC的面积.
如图所示,已知在△ABC中,∠A=30°,∠B=135°,AC=8.求△ABC的面积.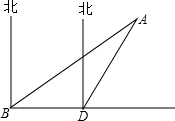 天然气管道铺设工程从B向正东方向进行,如图所示,从B处测得A点位于B点北偏东60°,从B向东前进400m到达D点,在D点测得A点位于北偏东45°方向,以A点为中心,半径为500m的圆形区域为居民住宅区,请计算后回答:天然气管道铺设工程是否会穿过居民住宅区?(
天然气管道铺设工程从B向正东方向进行,如图所示,从B处测得A点位于B点北偏东60°,从B向东前进400m到达D点,在D点测得A点位于北偏东45°方向,以A点为中心,半径为500m的圆形区域为居民住宅区,请计算后回答:天然气管道铺设工程是否会穿过居民住宅区?(