题目内容
10. 如图:已知在Rt△ABC中,∠ACB=90°,CD⊥AB,FE⊥AB,垂足为ID、E.
如图:已知在Rt△ABC中,∠ACB=90°,CD⊥AB,FE⊥AB,垂足为ID、E.(1)说明:△AFE∽△CBD;
(2)图中除△AFE外,与△CBD相似的还有哪些三角形?
(3)说明:BC2=BD•AB.
分析 (1)先利用等角的余角相等得到∠A=∠BCD,然后根据有两组角对应相等的两个三角形相似可得到结论;
(2)根据有两组角对应相等的两个三角形相似即可得到结论;
(3)根据相似三角形的性质即可得到结论.
解答 (1)证明:∵CD⊥AB,FE⊥AB,
∴∠ADC=90°,∠AEF=90°,
∴∠A+ACD=90°,
而∠BCD+ACD=90°,
∴∠A=∠BCD,
而∠AEF=∠BDC,
∴△AFE∽△CBD;
(2)∵∠A=∠BCD,∠ACB=∠BDC=∠ADC=90°,
∴△BDC∽△ACB∽△ACD,
∴除△AFE外,与△CBD相似的还有△ACB,△ADC;
(3)∵△BCD∽△ACB,
∴$\frac{BC}{AB}=\frac{BD}{BC}$,
∴BC2=BD•AB.
点评 本题考查了相似三角形的判定和性质,余角的性质,熟记有两组角对应相等的两个三角形相似是解题的关键.

练习册系列答案
相关题目
1.在-π,3.1415,2.121221,-$\frac{5}{6}$,-0.$\stackrel{•}{5}$$\stackrel{•}{7}$中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.已知y=x2+(t-2)x-2,当x>1时y随x的增大而增大,则t的取值范围是( )
| A. | t>0 | B. | t=0 | C. | t<0 | D. | t≥0 |

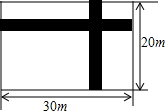 如图,在宽为20m,长为30m的矩形场地上,修筑同样宽的两条道路,余下的部分作为耕地,要使耕地的面积为500m2,若设路宽为x m,试计算路的宽度.
如图,在宽为20m,长为30m的矩形场地上,修筑同样宽的两条道路,余下的部分作为耕地,要使耕地的面积为500m2,若设路宽为x m,试计算路的宽度.