题目内容
20．
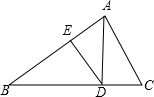如图：AD是Rt△ABC斜边BC上的高，DE是△ABD的AB边上的高，则图中与△ABC相似的三角形的个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据相似三角形的判定定理，利用已知条件判定相似的三角形的个数即可．
解答 解：∵AD是Rt△ABC斜边BC上的高，DE是△ABD的AB边上的高，
∴AC⊥AB，DE⊥AB，
∴DE∥AC，
∴△BED∽△BAC．
在直角△ABD中，AD⊥BD，DE⊥AB．
∵∠B=∠B，∠BED=∠BDA，
∴△BED∽△BDA；
同理，△AED∽△ADB，
∴△BDA∽△BAC，△ADB∽△ABC．
在直角△ABC中，AD⊥BC，AB⊥AC．则△ACD∽△BCA．
综上所述，图中与△ABC相似的三角形分别是：△BED、△AED、△BDA、△ACD．共有4个．
故选：B．
点评 此题主要考查学生对相似三角形的判定方法的掌握情况．
平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；
（2）三边法：三组对应边的比相等的两个三角形相似；
（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；
（4）两角法：有两组角对应相等的两个三角形相似．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
10．等边三角形面积为8$\sqrt{3}$cm，则它的边长（ ）
| A． | 2$\sqrt{2}$cm | B． | 4$\sqrt{2}$cm | C． | 8$\sqrt{2}$cm | D． | 以上结论都不对 |
11．下列各式中，从等号左边变形至等号右边一定成立的是（ ）
| A． | $\frac{a+b}{{a}^{2}b}$=$\frac{ac+bc}{{a}^{2}bc}$ | B． | $\frac{2x}{{x}^{2}{+y}^{2}}$=$\frac{2x+1}{{x}^{2}{+y}^{2}+1}$ | ||
| C． | $\frac{2x}{{x}^{2}y+xy}$=$\frac{2}{xy+y}$ | D． | $\frac{{x}^{2}{+y}^{2}}{x+y}$=xy |
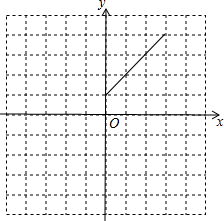我们知道，把直线y=x向左平移1个单位可得到一次函数y=x+1的图象，把直线y=kx（k≠0）向左平移1个单位可得到一次函数y=k（x+1）的图象，把抛物线y=ax2（a≠0）向左平移1个单位，可得到二次函数y=a（x+1）2的图象．
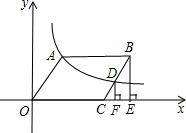如图，在平面直角坐标系中，?OABC顶点A，B在第一象限，顶点C在x轴正半轴上，反比例函数y=$\frac{k}{x}$（x＞0）的图象过点A，交BC于点D，BE⊥x轴于E，DE⊥x轴于F．设△ODF的面积为S1，四边形BEFD的面积为S2，则S1与S2的大小关系为相等．