题目内容
8.计算:(1)($\sqrt{18}$-$\sqrt{50}$+3$\sqrt{8}$)÷$\sqrt{2}$
(2)$\sqrt{12}$-($\sqrt{3}$+1)2+$\sqrt{\frac{3}{4}}$.
分析 (1)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的乘法运算;
(2)先根据完全平方公式计算,再把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=(3$\sqrt{2}$-5$\sqrt{2}$+6$\sqrt{2}$)÷$\sqrt{2}$
=4$\sqrt{2}$÷$\sqrt{2}$
=4;
(2)原式=2$\sqrt{3}$-(3+2$\sqrt{3}$+1)+$\frac{\sqrt{3}}{2}$
=2$\sqrt{3}$-4-2$\sqrt{3}$+$\frac{\sqrt{3}}{2}$
=-4+$\frac{\sqrt{3}}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
16.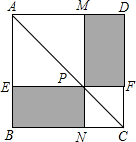 如图,在正方形ABCD中,P是线段AC上任意一点,过点P分别作EF∥AD,MN∥AB.设正方形AEPM和正方形CFPN的面积之和为S1,其余部分(即图中两阴影部分)的面积之和为S2,则S1与S2的大小关系是( )
如图,在正方形ABCD中,P是线段AC上任意一点,过点P分别作EF∥AD,MN∥AB.设正方形AEPM和正方形CFPN的面积之和为S1,其余部分(即图中两阴影部分)的面积之和为S2,则S1与S2的大小关系是( )
 如图,在正方形ABCD中,P是线段AC上任意一点,过点P分别作EF∥AD,MN∥AB.设正方形AEPM和正方形CFPN的面积之和为S1,其余部分(即图中两阴影部分)的面积之和为S2,则S1与S2的大小关系是( )
如图,在正方形ABCD中,P是线段AC上任意一点,过点P分别作EF∥AD,MN∥AB.设正方形AEPM和正方形CFPN的面积之和为S1,其余部分(即图中两阴影部分)的面积之和为S2,则S1与S2的大小关系是( )| A. | S1>S2 | B. | S1≥S2 | C. | S1<S2 | D. | S1≤S2 |
18.△ABC中,AB=AC,BC=8,则△ABC的周长x的取值范围是( )
| A. | x>4 | B. | 8<x<16 | C. | 16<x<24 | D. | x>16 |
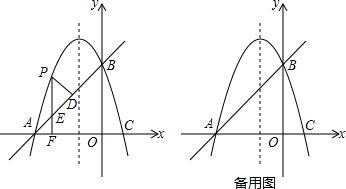
 如图是某几何体的三视图,则这个几何体的表面积是3π.
如图是某几何体的三视图,则这个几何体的表面积是3π.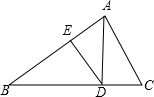 如图:AD是Rt△ABC斜边BC上的高,DE是△ABD的AB边上的高,则图中与△ABC相似的三角形的个数是( )
如图:AD是Rt△ABC斜边BC上的高,DE是△ABD的AB边上的高,则图中与△ABC相似的三角形的个数是( )