题目内容
15.(1)如图1,△ABC中,AD平分∠BAC交BC于点D,在AB上截取AE=AC,过点E作EF∥BC交AD于点F.求证:四边形CDEF是菱形;(2)如图2,△ABC中,AD平分△ABC的外角∠EAC交BC的延长线于点D,在BA的延长线上截取AE=AC,过点E作EF∥BC交DA的延长线于点F.四边形CDEF还是菱形吗?如果是,请证明;如果不是,请说明理由.
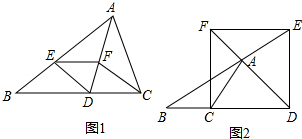
分析 (1)直接由SAS得出△ADE≌△ADC,进而得出DE=DC,∠ADE=∠ADC.再由SAS证明△AFE≌△AFC,得出EF=CF.由EF∥BC得出∠EFD=∠ADC,从而∠EFD=∠ADE,根据等角对等边得出DE=EF,从而DE=EF=CF=DC,由菱形的判定可知四边形CDEF是菱形.
(2)首先由SAS证出△ADE≌△ADC,△AFE≌△AFC,得出DE=DC,∠ADE=∠ADC,EF=CF.然后由EF∥BC,得出∠EFD=∠ADC,从而∠EFD=∠ADE,根据等边对等角得出DE=EF,则DE=EF=CF=DC,由菱形的判定可知四边形CDEF是菱形.
解答 (1)证明:在△ADE和△ADC中,
∵$\left\{\begin{array}{l}{AE=AC}\\{∠EAF=∠CAF}\\{AD=AD}\end{array}\right.$
∴△ADE≌△ADC(SAS);
∴DE=DC,∠ADE=∠ADC
同理△AFE≌△AFC,
∴EF=CF
∵EF∥BC
∴∠EFD=∠ADC,
∴∠EFD=∠ADE,
∴DE=EF,
∴DE=EF=CF=DC,
∴四边形CDEF是菱形.
(2)解:四边形CDEF是菱形.理由如下:
在△ADE和△ADC中,
∵$\left\{\begin{array}{l}{AE=AC}\\{∠EAF=∠CAF}\\{AD=AD}\end{array}\right.$
∴△ADE≌△ADC(SAS),
∴DE=DC,∠ADE=∠ADC.
同理△AFE≌△AFC,
∴EF=CF.
∵EF∥BC,
∴∠EFD=∠ADC,
∴∠EFD=∠ADE,
∴DE=EF,
∴DE=EF=CF=DC,
∴四边形CDEF是菱形.
点评 本题主要考查了全等三角形的判定与性质、菱形的判定、平行线等知识,正确利用全等三角形的判定与性质得出是解题关键.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案 如图,A(4,0),B(0,4)两点,P在BA延长线上,△OPE为等腰直角三角形,F为PE的中点,OF交AB于M.
如图,A(4,0),B(0,4)两点,P在BA延长线上,△OPE为等腰直角三角形,F为PE的中点,OF交AB于M. 如图物体是由6个相同的小正方体搭成的,请你画出从正面、上面、左面看它所得到的平面图形.
如图物体是由6个相同的小正方体搭成的,请你画出从正面、上面、左面看它所得到的平面图形. 如图是某几何体的三视图,则这个几何体的表面积是3π.
如图是某几何体的三视图,则这个几何体的表面积是3π.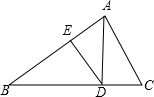 如图:AD是Rt△ABC斜边BC上的高,DE是△ABD的AB边上的高,则图中与△ABC相似的三角形的个数是( )
如图:AD是Rt△ABC斜边BC上的高,DE是△ABD的AB边上的高,则图中与△ABC相似的三角形的个数是( )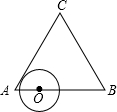 如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第4秒.
如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第4秒.