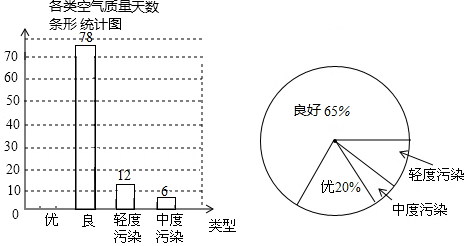
题目内容
2.计算:(1)$\sqrt{32}$-$\sqrt{50}$-4$\sqrt{\frac{1}{8}}$
(2)$\sqrt{6}$×$\sqrt{2}$+$\sqrt{24}$÷$\sqrt{3}$-$\sqrt{48}$.
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)先进行二次根式的2乘除运算,然后化简后合并即可.
解答 解:(1)原式=4$\sqrt{2}$-5$\sqrt{2}$-$\sqrt{2}$
=-2$\sqrt{2}$;
(2)原式=$\sqrt{2×6}$+$\sqrt{24÷3}$-4$\sqrt{2}$
=2$\sqrt{3}$+2$\sqrt{2}$-4$\sqrt{2}$
=2$\sqrt{3}$-2$\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
10.使分式$\frac{2}{{x}^{2}-4}$有意义的x取值范围是( )
| A. | x≠2 | B. | x≠-2 | C. | x≠2且x≠-2 | D. | x≠2或x≠-2 |

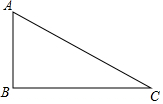 如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.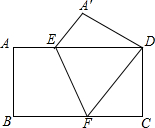 如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.
如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.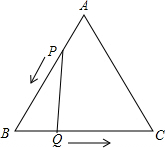 已知:如图,△ABC是边长为4cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题:
已知:如图,△ABC是边长为4cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: