题目内容
11.计算:(-1)2016+$\root{3}{8}$-3+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$.分析 先根据数的乘方与开方法则分别计算出各数,再根据实数混合运算的法则进行计算即可.
解答 解:原式=1+2-3+1
=3-3+1
=1.
点评 本题考查的是实数的运算,在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.小晨和小冰两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了100次实验,实验的结果如下:
(1)计算“2点朝上”的频率和“3点朝上”的频率;
(2)小晨说:“根据实验,一次实验中出现4点朝上的概率是$\frac{1}{4}$;”小晨的这一说法正确吗?为什么?
(3)小冰说:“根据实验,如果掷1000次,那么出现5点朝上的次数是200次.”小冰的这一说法正确吗?为什么?
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 10 | 15 | 20 | 25 | 20 | 10 |
(2)小晨说:“根据实验,一次实验中出现4点朝上的概率是$\frac{1}{4}$;”小晨的这一说法正确吗?为什么?
(3)小冰说:“根据实验,如果掷1000次,那么出现5点朝上的次数是200次.”小冰的这一说法正确吗?为什么?
6.下列能判定△ABC为等腰三角形的是( )
| A. | AB=AC=3,BC=6 | B. | ∠A=40°、∠B=70° | ||
| C. | AB=3、BC=8,周长为16 | D. | ∠A=40°、∠B=50° |
3.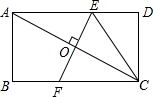 如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
 如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )| A. | 3 | B. | 3.5 | C. | 2.5 | D. | 2.8 |
20.如图1,A、B、C是三个垃圾存放点,点B、C分别位于点A的正北和正东方向,AC=100米,四人分别测得∠C的度数如表:
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:
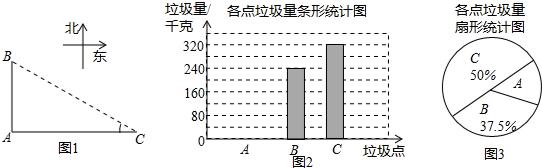
(1)求表中∠C度数的平均数$\overline{x}$;
(2)求A处的垃圾量,并将不完整的统计图2、3补充完整;
(3)用(1)中的$\overline{x}$作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
| 甲 | 乙 | 丙 | 丁 | |
| ∠C(单位:度) | 34 | 36 | 38 | 40 |

(1)求表中∠C度数的平均数$\overline{x}$;
(2)求A处的垃圾量,并将不完整的统计图2、3补充完整;
(3)用(1)中的$\overline{x}$作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
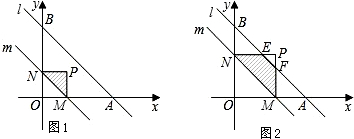
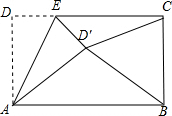 如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中:
如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中: