题目内容
20.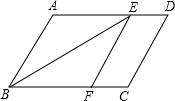 已知:如图,在?ABCD中,AD>AB,∠ABC的平分线交AD于点E,EF∥AB交BC于点F.四边形ABFE是菱形吗?请说明理由.
已知:如图,在?ABCD中,AD>AB,∠ABC的平分线交AD于点E,EF∥AB交BC于点F.四边形ABFE是菱形吗?请说明理由.
分析 根据平行四边形的性质得出AD∥BC,求出四边形ABFE是平行四边形,求出AB=AE,根据菱形的判定得出即可.
解答 解:四边形ABFE是菱形,
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,即AE∥BF,
∵EF∥AB,
∴四边形ABFE是平行四边形,
∵AE∥BF,
∴∠AEB=∠ABE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∴平行四边形ABFE是菱形.
点评 本题考查了菱形的性质和判定,平行四边形的性质和判定,等知识,能综合运用性质和判定进行推理是解此题的关键.

练习册系列答案
相关题目
10. 如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )
如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )
 如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )
如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )| A. | $\sqrt{10}$-1 | B. | $\sqrt{5}$-1 | C. | 2 | D. | $\sqrt{5}$ |
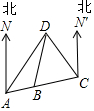 “奔跑吧,兄弟!”节目组,预设计一个新的游戏,“奔跑”需经A,B,C,D四点,如图,其中A,B,C三地在同一直线上,D点在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.
“奔跑吧,兄弟!”节目组,预设计一个新的游戏,“奔跑”需经A,B,C,D四点,如图,其中A,B,C三地在同一直线上,D点在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.