题目内容
10. 如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )
如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为( )| A. | $\sqrt{10}$-1 | B. | $\sqrt{5}$-1 | C. | 2 | D. | $\sqrt{5}$ |
分析 根据勾股定理,可得AC的长,根据圆的性质,可得答案.
解答 解:由勾股定理,得
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{10}$,
AM=AC=$\sqrt{10}$,
M点的坐标是$\sqrt{10}$-1,
故选:A.
点评 本题考查了实数与数轴,利用勾股定理得出AC的长是解题关键,注意M点的坐标是$\sqrt{10}$-1.

练习册系列答案
相关题目
1. 如图所示的几何体,从左面看是( )
如图所示的几何体,从左面看是( )
 如图所示的几何体,从左面看是( )
如图所示的几何体,从左面看是( )| A. |  | B. |  | C. |  | D. |  |
18.已知A,B,C是直线l上三点,线段AB=6cm,且AB=$\frac{1}{2}$AC,则BC=( )
| A. | 6cm | B. | 12cm | C. | 18cm | D. | 6cm或18cm |
7.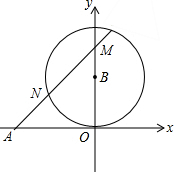 如图,已知A(-2,0),以B(0,1)为圆心,OB长为半径作⊙B,N是⊙B上一个动点,直线AN交y轴于M点,则△AOM面积的最大值是( )
如图,已知A(-2,0),以B(0,1)为圆心,OB长为半径作⊙B,N是⊙B上一个动点,直线AN交y轴于M点,则△AOM面积的最大值是( )
 如图,已知A(-2,0),以B(0,1)为圆心,OB长为半径作⊙B,N是⊙B上一个动点,直线AN交y轴于M点,则△AOM面积的最大值是( )
如图,已知A(-2,0),以B(0,1)为圆心,OB长为半径作⊙B,N是⊙B上一个动点,直线AN交y轴于M点,则△AOM面积的最大值是( )| A. | 2 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
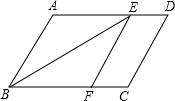 已知:如图,在?ABCD中,AD>AB,∠ABC的平分线交AD于点E,EF∥AB交BC于点F.四边形ABFE是菱形吗?请说明理由.
已知:如图,在?ABCD中,AD>AB,∠ABC的平分线交AD于点E,EF∥AB交BC于点F.四边形ABFE是菱形吗?请说明理由.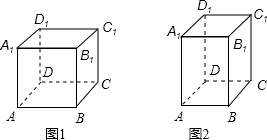
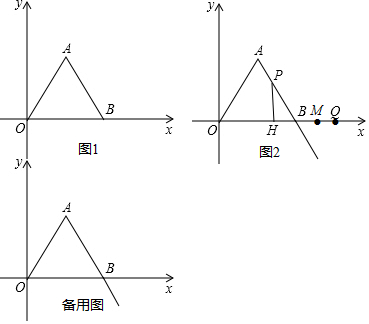
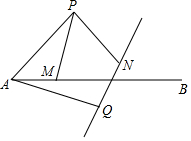 如图,点P在射线AB的上方,且∠PAB=45°,PA=2,点M是射线AB上的动点(点M不与点A重合),现将点P绕点A按顺时针方向旋转60°,到点Q,将点M绕点P按逆时针方向旋转60°到点N,连结AQ,PM,PN,作直线QN.
如图,点P在射线AB的上方,且∠PAB=45°,PA=2,点M是射线AB上的动点(点M不与点A重合),现将点P绕点A按顺时针方向旋转60°,到点Q,将点M绕点P按逆时针方向旋转60°到点N,连结AQ,PM,PN,作直线QN.