题目内容
15. 如图,已知点O(0,0),A(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为B.
如图,已知点O(0,0),A(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为B.(1)若l经过点A,求它的解析式,并写出此时l的对称轴及顶点坐标;
(2)设点B的纵坐标yB,求yB的最大值,此时l上有两点(x1,y1),(x2,y2),其中x1>x2≥0,比较y1与y2的大小.
分析 ,(1)把A(2,1)代入二次函数的解析式计算,得到解析式,根据二次函数的性质得到抛物线l的对称轴及顶点坐标;
(2)根据坐标的特征求出yB,根据平方的非负性求出yB的最大值,根据二次函数的性质比较y1与y2的大小即可.
解答 解:(1)把A(2,1)代入y=-(x-h)2+1,
得:-(2-h)2+1=1,
解得:h=2,
∴解析式为:y=-(x-2)2+1,
∴对称轴为:x=2,顶点坐标为:(2,1);
(2)点B的横坐标为0,则yB=-h2+1,
∴当h=0时,yB有最大值为1,
此时,抛物线为:y=-x2+1,对称轴为y轴,
当x≥0时,y随着x的增大而减小,
∴x1>x2≥0时,y1<y2.
点评 本题考查的是二次函数的最值的确定、待定系数法的应用,灵活运用待定系数法求出二次函数的解析式、熟记二次函数的性质是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
6. 如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
 如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )| A. | 100° | B. | 112.5° | C. | 120° | D. | 135° |
 如图,△ABD内接于⊙O,BC为⊙O的直径,∠A=40°,∠ABD=75°,则∠ABC=25°.
如图,△ABD内接于⊙O,BC为⊙O的直径,∠A=40°,∠ABD=75°,则∠ABC=25°. 如图,这是某市部分简图(图中小正方形的边长代表1km长).以火车站为坐标原点建立平面直角坐标系.
如图,这是某市部分简图(图中小正方形的边长代表1km长).以火车站为坐标原点建立平面直角坐标系. 已知:如图,∠1=∠2,∠C=∠D.
已知:如图,∠1=∠2,∠C=∠D.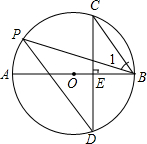 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.