题目内容
16．
如图，一块平面反光镜在∠AOB的边OA上，∠AOB=40°，在OB上有一点P，从P点射出一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行，由科学实验知道：∠OQP=∠AQR，求∠QPB的度数．
分析 由QR∥OB，∠AOB=40°，根据两直线平行，同位角相等，即可求得∠AQR的度数，又由∠AOB的两边OA，OB都为平面反光镜，根据反射的性质，可得∠OQP=∠AQR=40°，然后又三角形外角的性质，求得∠QPB的度数．
解答 解：∵QR∥OB，∠AOB=40°，
∴∠AQR=∠AOB=40°，
∵∠AOB的两边OA，OB都为平面反光镜，
∴∠OQP=∠AQR=40°，
∴∠QPB=∠AOB+∠OQP=40°+40°=80°．
点评 此题考查了平行线的性质、三角形外角的性质以及反射的性质．此题难度不大，注意掌握两直线平行，同位角相等定理的应用，注意数形结合思想的应用．
练习册系列答案
相关题目
4．下列各式从左边到右边的变形，属于因式分解的是（ ）
| A． | （x+y）2=x2+2xy+y2 | B． | 2x2-8=2（x+2）（x-2） | ||
| C． | 2x2-2x+1=2x（x-1）+1 | D． | （x+1）（x-1）=x2-1 |
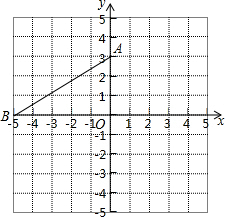如图，在平面直角坐标系中，点A的坐标是（0，3），点B在x轴的负半轴上，将△AOB绕点A逆时针旋转90°得到△AEF，点O，B的对应点分别为E，F．
1．代数式4x2+ax+9是个完全平方式，则a的值为（ ）
| A． | 6 | B． | ±6 | C． | 12 | D． | ±12 |
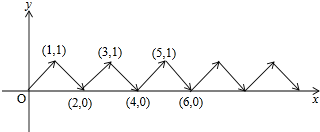如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，1），…，按这样的运动规律，经过第2016次运动后，点P运动的总长度是2016$\sqrt{2}$．
5．
如图，将矩形ABCD沿AE对折，使点D落在点F处，若∠CEF=60°，则∠EAF等于（ ）
如图，将矩形ABCD沿AE对折，使点D落在点F处，若∠CEF=60°，则∠EAF等于（ ）| A． | 60° | B． | 50° | C． | 40° | D． | 30° |