题目内容
1.若ab=1,m=$\frac{1}{1+a}$+$\frac{1}{1+b}$,则(-m)2016的值为1.分析 根据异分母分式的加法计算得m=$\frac{2+a+b}{1+a+b+ab}$,将ab=1代入得m=1,继而可得答案.
解答 解:当ab=1时,
m=$\frac{1+b+1+a}{(1+a)(1+b)}$
=$\frac{2+a+b}{1+a+b+ab}$
=$\frac{2+a+b}{2+a+b}$
=1,
则(-m)2016=(-1)2016=1,
故答案为:1.
点评 本题主要考查分式的化简求值,根据异分母分式的加法计算求得m的值是解题的关键.

练习册系列答案
相关题目
9.下列各式是二元一次方程的是( )
| A. | 3y+$\frac{1}{2}x$ | B. | $\frac{x+y}{3}-2y=0$ | C. | y=$\frac{2}{x}+1$ | D. | x2+y=0 |
10.长沙到娄底的铁路长约为180千米,动车运行后的平均速度是原来火车速度的1.8倍,这样由长沙到娄底的行驶时间缩短了1.2小时,设原来火车的平均每小时行驶X千米,则下列方程正确的是( )
| A. | $\frac{180}{x}$-1.8=$\frac{180}{1.2x}$ | B. | $\frac{180}{x}$+1.8=$\frac{180}{1.2x}$ | ||
| C. | $\frac{180}{x}$-1.2=$\frac{180}{1.8x}$ | D. | $\frac{180}{x}$+1.2=$\frac{180}{1.8x}$ |
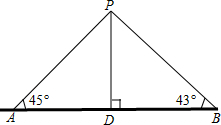 如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)
如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m) 如图,海面上以点A为中心的4海里内有暗礁,在海面上点B处有一艘海监船,欲到C处去执行任务,若∠ABC=45°,∠ACB=37°,B,C两点相距10海里,如果这艘海监船沿BC直接航行,会有触礁的危险吗?请说明理由.
如图,海面上以点A为中心的4海里内有暗礁,在海面上点B处有一艘海监船,欲到C处去执行任务,若∠ABC=45°,∠ACB=37°,B,C两点相距10海里,如果这艘海监船沿BC直接航行,会有触礁的危险吗?请说明理由.