题目内容
11.如果关于x的方程$\frac{a}{x+3}$$+\frac{1}{x-3}$=$\frac{3+a}{{x}^{2}-9}$无解,则a的值为-1或3或-$\frac{3}{7}$.分析 去分母化分式方程为整式方程可得(a+1)x=4a,当a+1=0时,方程无解;当a+1≠0时,x=$\frac{4a}{a+1}$,由分式方程无解可得$\frac{4a}{a+1}$=3或$\frac{4a}{a+1}$=-3解方程得a的值.
解答 解:方程两边都乘以最简公分母(x+3)(x-3),得:a(x-3)+x+3=3+a,
整理,得:(a+1)x=4a,
①当a+1=0,即a=-1时,方程无解;
②当a+1≠0时,x=$\frac{4a}{a+1}$,
由分式方程无解可得$\frac{4a}{a+1}$=3或$\frac{4a}{a+1}$=-3,
解得:a=3或a=-$\frac{3}{7}$,
综上,a=-1或a=3或a=-$\frac{3}{7}$,
故答案为:-1或3或-$\frac{3}{7}$.
点评 本题主要考查分式方程的解和解分式方程,由方程无解分类讨论且得出关于a的方程是解题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
16.下列方程中是二元一次方程的是( )
| A. | 3x+y=0 | B. | 2x-1=4 | C. | 2x2-y=2 | D. | 2x+y=3z |
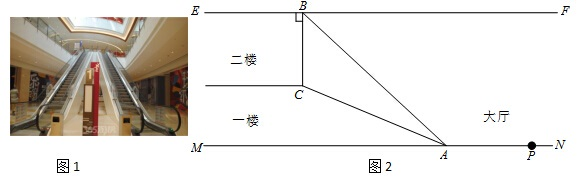
 保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3) +(
+( )?1?2cos60?; (2)(2x?y)2?(x+y)(x?y) .
)?1?2cos60?; (2)(2x?y)2?(x+y)(x?y) .