题目内容
6. 如图,海面上以点A为中心的4海里内有暗礁,在海面上点B处有一艘海监船,欲到C处去执行任务,若∠ABC=45°,∠ACB=37°,B,C两点相距10海里,如果这艘海监船沿BC直接航行,会有触礁的危险吗?请说明理由.
如图,海面上以点A为中心的4海里内有暗礁,在海面上点B处有一艘海监船,欲到C处去执行任务,若∠ABC=45°,∠ACB=37°,B,C两点相距10海里,如果这艘海监船沿BC直接航行,会有触礁的危险吗?请说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 作AM⊥BC于M,证出△ABM是等腰直角三角形,得出AM=BM,设AM=BM=x海里,则CM=10-x(海里),在Rt△ACM中,由三角函数得出方程,解方程即可.
解答 解:如果这艘海监船沿BC直接航行,不会有触礁的危险;理由如下: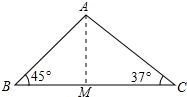
作AM⊥BC于M,如图所示:
∵∠ABC=45°,
∴△ABM是等腰直角三角形,
∴AM=BM,设AM=BM=x海里,则CM=10-x(海里),
在Rt△ACM中,$\frac{AM}{CM}$=tan∠ACB=tan37°≈0.75,
∴$\frac{x}{10-x}=\frac{3}{4}$,
解得:x=$\frac{30}{7}$,
经检验,x=$\frac{30}{7}$是方程的根,
∴AM=$\frac{30}{7}$海里>4海里,
∴如果这艘海监船沿BC直接航行,不会有触礁的危险.
点评 本题考查了解直角三角形、等腰直角三角形的判定与性质、解方程;熟练掌握解直角三角形,由三角函数得出方程是解决问题的关键.

练习册系列答案
相关题目
16.下列方程中是二元一次方程的是( )
| A. | 3x+y=0 | B. | 2x-1=4 | C. | 2x2-y=2 | D. | 2x+y=3z |
14.已知x-$\frac{1}{x}=3$,则x2$+\frac{1}{{x}^{2}}$的值是( )
| A. | 9 | B. | 7 | C. | 11 | D. | 不能确定 |
18. 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
(1)本次调查的样本为200名初中毕业生的视力情况,样本容量为200;
(2)在频数分布表中,a=60,b=0.05,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)在频数分布表中,a=60,b=0.05,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?