题目内容
16.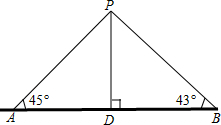 如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)
如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)【参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93】
分析 设PD=xm,证出△PAD是等腰直角三角形,得出AD=PD=x,在Rt△PBD中,由三角函数得出DB=$\frac{x}{0.93}$,由题意得出方程,解方程即可.
解答 解:设PD=xm,
∵PD⊥AB,
∴∠ADP=∠BDP=90°,
在Rt△PAD中,∠PAD=45°,
∴AD=PD=x,
在Rt△PBD中,tan∠PBD=$\frac{x}{DB}$,
∴DB=$\frac{x}{tan43°}$=$\frac{x}{0.93}$,
∵AB=80,
∴x+$\frac{x}{0.93}$=80,
解得:x≈38.5,即PD=38.5米;
答:小桥PD的长为38.5米.
点评 本题考查了解直角三角形、等腰直角三角形的判定与性质、解方程;熟练掌握解直角三角形,由三角函数得出方程是解决问题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
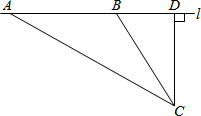 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°. 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片